题目内容
19.问题:如图1,DE∥GB,DE=GB,BD与EG相交于点F,证明:△DEF≌△BGF.
拓展一:
如图2,在△ACB和△AED中,点E在AC上,AC=BC,AE=DE,∠DEA=∠BCA=90°,连接BD,取BD中点F,连接FE、FC,请你探究CF和EF之间的位置关系和数量关系.
拓展二:
如图3,四边形ABCD∽四边形BEFG,点E在AB的延长线上,P是线段DF的中点,连接CP、PG,若CP⊥PG,则四边形ABCD应满足的条件是菱形;若CP⊥PG、且PC=$\sqrt{3}$PG,则四边形ABCD应满足的条件是菱形且∠A=60°.

分析 问题:根据品牌形象的性质得到∠D=∠B,∠E=∠G,然后根据全等三角形的判定即可得到结论.
拓展一:连接CF,直角△DEB中,EF是斜边BD上的中线,因此EF=DF=BF,∠FEB=∠FBE,同理可得出CF=DF=BF,∠FCB=∠FBC,因此CF=EF,由于∠DFE=∠FEB+∠FBE=2∠FBE,同理∠DFC=2∠FBC,因此∠EFC=∠EFD+∠DFC=2(∠EBF+∠CBF)=90°,因此△EFC是等腰直角三角形,CF=$\sqrt{2}$EF;
拓展二:可证三角形DHP和PGF全等,已知的有DC∥GF,根据平行线间的内错角相等可得出两三角形中两组对应的角相等,又有DP=PF,因此构成了全等三角形判定条件中的(ASA),于是两三角形全等,那么HP=PG,可根据三角函数来得出PG、CG的比例关系.
解答 问题:证明:∵DE∥GB,
∴∠D=∠B,∠E=∠G,
在△DEF和△BGF中,
$\left\{\begin{array}{l}{∠D=∠B}\\{DE=BG}\\{∠E=∠G}\end{array}\right.$,
∴△DEF≌△BGF.
拓展一:解:如图,连结CF、AF,
∵AC=BC,AE=DE,∠DEA=∠BCA=90°,
∴∠DAE=∠CAB=45°,
∴∠BAD=∠BAC+∠DAE=45°+45°=90°,
又∵点F是BD的中点,
∴FA=FB=FD,
在△ACF和△BCF中,$\left\{\begin{array}{l}{FA=FB}\\{AC=BC}\\{CF=CF}\end{array}\right.$,
∴△ACF≌△BCF,
∴∠ACF=∠BCF=$\frac{1}{2}$∠ACB=45°,
∵FA=FB,CA=CB,
∴CF所在的直线垂直平分线段AB,
同理,EF所在的直线垂直平分线段AD,
又∵DA⊥BA,
∴EF⊥CF,
∴△CEF为等腰直角三角形,
∴CE=EF;
拓展二:解:若CP⊥PG,四边形ABCD是菱形,
如图3,
设GP交DC交于点H,
∵四边形ABCD∽四边形BEFG,
∴四边形BFEG是菱形,
∵P是线段DF的中点,
∴FP=DP,
由题意可知DC∥GF,
∴∠GFP=∠HDP,
在△GFP和△HDP中$\left\{\begin{array}{l}{∠GPF=∠HPD}\\{PF=DP}\\{∠GFP=∠HDP}\end{array}\right.$,
∴△GFP≌△HDP(ASA),
∴GP=HP,GF=HD,
∵四边形ABCD是菱形,
∴CD=CB,
∴CG=CH,
∴△CHG是等腰三角形,
∴PG⊥PC;
若CP⊥PG、且PC=$\sqrt{3}$PG,四边形ABCD是菱形,且∠A=60°,
∵∠DCB=∠A=60°,
∴∠PCG=30°,
∴∠CGP=60°,
∴tan∠PGC=$\frac{PC}{PG}$=$\sqrt{3}$,
∴PC=$\sqrt{3}$PG.
故答案为:菱形,菱形,∠A=60°.
点评 本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.也考查了全等三角形的判定与性质和等腰三角形的性质.

 阅读快车系列答案
阅读快车系列答案| A. | (-2,1) | B. | (1,-2) | C. | (-2,-2) | D. | (1,2) |
| A. | 300名考生的数学成绩 | B. | 300 | ||
| C. | 1.33万名考生的数学成绩 | D. | 300名考生 |
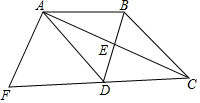 如图,四边形ABCD中,BD垂直平分AC,垂足为点E,点F为四边形ABCD外一点,DA平分∠BDF,∠ADF=∠BAD,且AF⊥AC.
如图,四边形ABCD中,BD垂直平分AC,垂足为点E,点F为四边形ABCD外一点,DA平分∠BDF,∠ADF=∠BAD,且AF⊥AC. 如图,已知?ABCD中,对角线AC与BD交于点O,∠ABD=2∠DBC,AE⊥BD于E.
如图,已知?ABCD中,对角线AC与BD交于点O,∠ABD=2∠DBC,AE⊥BD于E.