题目内容
16.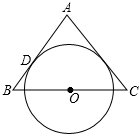 如图,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于点D.
如图,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于点D.(1)求证:AC是⊙O的切线.
(2)已知:∠BAC=120°,BC=12,求⊙O的半径是多少?
分析 (1)过点O作OE⊥AC于点E,连结OD,OA,根据切线的性质得出AB⊥OD,根据等腰三角形三线合一的性质得出AO是∠BAC的平分线,根据角平分线的性质得出OE=OD,从而证得结论;
(2)由等腰三角形的性质“三线合一”可得OB,由切线的性质可得∠BAO,可得∠B,由含30°角直角三角形的性质可得BD的长,进而求出DO的长.
解答 (1)证明:过点O作OE⊥AC于点E,连结OD,OA,
∵AB与⊙O相切于点D,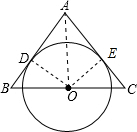
∴AB⊥OD,
∵△ABC为等腰三角形,O是底边BC的中点,
∴AO是∠BAC的平分线,
∴OE=OD,即OE是⊙O的半径,
∵AC经过⊙O的半径OE的外端点且垂直于OE,
∴AC是⊙O的切线;
(2)解:∵△ABC为等腰三角形,O是底边BC的中点,BC=12,
∴AO⊥BC,BO=6,
∵∠BAC=120°,AB,AC为⊙O的切线,
∴∠BAO=∠CAO=60°,
∴∠B=30°,
∵BO=6,∠B=30°,OD⊥AB,
∴BD=$\frac{1}{2}OB=\frac{1}{2}×6=3$,
则DO=3$\sqrt{3}$,
∴⊙O的半径是3$\sqrt{3}$.
点评 考查了切线的判定和性质,等腰三角形的性质,直角三角形的性质,熟练掌握性质定理是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
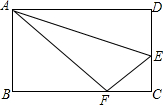 如图,把边长AD=10,AB=8的矩形沿AE对折,使点D落在BC上的点F处,求DE之长.
如图,把边长AD=10,AB=8的矩形沿AE对折,使点D落在BC上的点F处,求DE之长. 如图:作出与△ABC关x轴对称的图形△A1B1C1,并写出各点的坐标:
如图:作出与△ABC关x轴对称的图形△A1B1C1,并写出各点的坐标: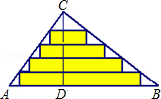 如图,△ABC是一张直角三角形彩色纸,∠ACB=90°,AC=30cm,BC=40cm,CD⊥AB于点D.
如图,△ABC是一张直角三角形彩色纸,∠ACB=90°,AC=30cm,BC=40cm,CD⊥AB于点D.