题目内容
11.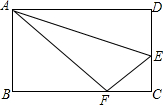 如图,把边长AD=10,AB=8的矩形沿AE对折,使点D落在BC上的点F处,求DE之长.
如图,把边长AD=10,AB=8的矩形沿AE对折,使点D落在BC上的点F处,求DE之长.
分析 在Rt△ABF中,由勾股定理可求得BF=6,故此FC=4,设DE=EF=x,则EC=8-x,在Rt△EFC中由勾股定理得:x2=42+(8-x)2,解得x=5.
解答 解:由翻折的性质可知:AF=AD=10、DE=EF.
在Rt△ABF中,BF=$\sqrt{A{F}^{2}-A{B}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6.
∵FC=BC-BF,
∴FC=4.
设DE=EF=x,则EC=8-x,在Rt△EFC中由勾股定理得:EF2=FC2+EC2,即x2=42+(8-x)2,
解得;x=5.
∴DE=5.
点评 本题主要考查的是翻折的性质、勾股定理的应用,依据勾股定理得到关于x的方程是解题的关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
19.关于x的一元二次方程x2-4x+2=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 无实数根 | D. | 有无实数根,无法判断 |
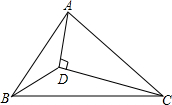 如图,在△ABC中,点D为△ABC内一点,连接AD,BD,CD,∠DBC=∠ACD=30°,∠ADC=90°,DB=3,BC=8,则AB的长为$\frac{10}{3}\sqrt{3}$.
如图,在△ABC中,点D为△ABC内一点,连接AD,BD,CD,∠DBC=∠ACD=30°,∠ADC=90°,DB=3,BC=8,则AB的长为$\frac{10}{3}\sqrt{3}$.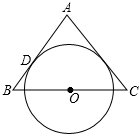 如图,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于点D.
如图,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于点D.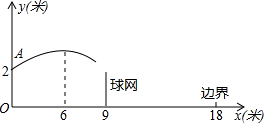 如图,排球运动员站在点O处练习发球,将球从点O正上方2米的点A处发出把球看成点,其运行的高度y(米)与运行的水平距离x(米)满足关系式y=a(x-6)2+2.6,已知球网与点O的水平距离为9米,高度为2.43米,球场的边界距点O的水平距离为18米.
如图,排球运动员站在点O处练习发球,将球从点O正上方2米的点A处发出把球看成点,其运行的高度y(米)与运行的水平距离x(米)满足关系式y=a(x-6)2+2.6,已知球网与点O的水平距离为9米,高度为2.43米,球场的边界距点O的水平距离为18米.