Question

11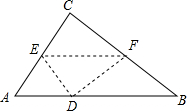．如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，翻折∠C，使点C落在斜边AB上某一点D处，折痕为EF（点E、F分别在边AC、BC上）．若△CEF与△ABC相似，则AD的长为$\frac{18}{5}$或5．

Answer 1

分析 若△CEF与△ABC相似，分两种情况：①若CE：CF=3：4，如图1所示，此时EF∥AB，CD为AB边上的高；②若CF：CE=3：4，如图2所示．由相似三角形角之间的关系，可以推出∠A=∠ECD与∠B=∠FCD，从而得到CD=AD=BD，即D点为AB的中点．

解答 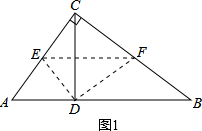解：若△CEF与△ABC相似，分两种情况：
①若CE：CF=3：4，如图1所示．
∵CE：CF=AC：BC，
∴EF∥AB．
由折叠性质可知，CD⊥EF，
∴CD⊥AB，即此时CD为AB边上的高．
在Rt△ABC中，∵∠ACB=90°，AC=6，BC=8，
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=10，
∴cosA=$\frac{AC}{AB}$=$\frac{6}{10}$=$\frac{3}{5}$，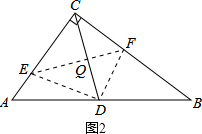
∴AD=AC•cosA=6×$\frac{3}{5}$=$\frac{18}{5}$；
②若CF：CE=3：4，如图2所示．
∵△CEF∽△CBA，
∴∠CEF=∠B．
由折叠性质可知，∠CEF+∠ECD=90°，
又∵∠A+∠B=90°，
∴∠A=∠ECD，
∴AD=CD．
同理可得：∠B=∠FCD，CD=BD，
∴D点为AB的中点，
∴AD=$\frac{1}{2}$AB=$\frac{1}{2}$×10=5．
故答案为：$\frac{18}{5}$或5．

点评 本题主要考查的是相似三角形的性质，折叠的性质，勾股定理和，难度适中，运用分类讨论及数形结合思想是解题的关键．