题目内容
如图，一矩形与⊙O相交，若AB=4，BC=6，DE=2，则DF=（ ）| A、13 | B、12 | C、11 | D、10 |
考点：垂径定理,勾股定理,矩形的性质
专题：计算题
分析：作OM⊥BC于M，如图，根据垂径定理得BM=CM=
BC=3，再证明四边形ADOM为矩形，得到OD=AM=AB+BM=7，则OE=OD-DE=5，所以OF=5，然后利用DF=OD+OF进行计算即可．
| 1 |
| 2 |
解答：解：作OM⊥BC于M，如图，
则BM=CM=
BC=3，
∵四边形ADHG为矩形，
∴∠A=∠D=90°，
∴四边形ADOM为矩形，
∴OD=AM=AB+BM=4+3=7，
∴OE=OD-DE=7-2=5，
∴OF=5，
∴DF=OD+OF=7+5=12．
故选B．
则BM=CM=| 1 |
| 2 |
∵四边形ADHG为矩形，
∴∠A=∠D=90°，
∴四边形ADOM为矩形，
∴OD=AM=AB+BM=4+3=7，
∴OE=OD-DE=7-2=5，
∴OF=5，
∴DF=OD+OF=7+5=12．
故选B．
点评：本题考查了垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．也考查了矩形的性质．
练习册系列答案
相关题目
下列各式中：
，2x4-1，7a+b，-2，
，
多项式有（ ）
| abc |
| 2 |
| a+b |
| 2 |
| m+n |
| m |
| A、2个 | B、3个 | C、4个 | D、5个 |
如图，△ADE∽△ACB，则DE：BC=
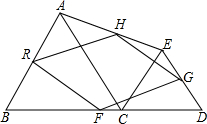已知：如图，C是线段BD上一点，△ABC和△ECD都是等边三角形，R、F、G、H分别是四边形ABDE各边的中点，求证：四边形RFGH是菱形．
如图所示，直线BC经过原点O，点A在x轴上，AD⊥BC于D，若B（m，2），C（n，-3），A（2，0），则AD•BC=
如图，已知实数a、b在数轴上的对应点的位置如图所示，化简：|b|-
如图，CD是Rt△ABC斜边上的高．
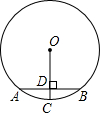如图，AB为⊙O的弦，⊙O的半径为5，OC⊥AB于点D，交⊙O于点C，且CD=1，则弦12．如图，AB为⊙O的弦，⊙O的半径为5，OC⊥AB于点D，交⊙O于点C，且CD=1，则弦AB的长是
如图在正方体的展开图上编号，请写出相对面（相对面没有公共棱）的号码：1对应