题目内容
 如图,在△ABC中,∠C=90°,∠A=25°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,求
如图,在△ABC中,∠C=90°,∠A=25°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,求 |
| BD |
考点:圆心角、弧、弦的关系
专题:计算题
分析:连结CD,如图,先根据三角形内角和计算出∠B=65°,再根据等腰三角形的性质由CB=CD得到∠B=∠BDC=65°,然后再利用三角形内角和计算出∠BCD=50°,最后根据圆心角的度数等于它所对的弧的度数求解.
解答:解:连结CD,如图,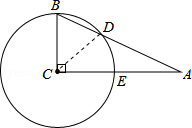
∵∠C=90°,∠A=25°,
∴∠B=90°-25°=65°,
∵CB=CD,
∴∠B=∠BDC=65°,
∴∠BCD=180°-65°-65°=50°,
∴
的度数为50°.

∵∠C=90°,∠A=25°,
∴∠B=90°-25°=65°,
∵CB=CD,
∴∠B=∠BDC=65°,
∴∠BCD=180°-65°-65°=50°,
∴
 |
| BD |
点评:本题考查了圆心角、弧、弦的关系:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等;圆心角的度数等于它所对的弧的度数.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
下列各式正确的是( )
| A、cos60°<sin45°<tan45° |
| B、sin45°<cos60°<tan45° |
| C、sin45°<tan45°<cos60 |
| D、cos60°<tan45°<sin45° |
在△ABC中,∠B的平分线与∠C的平分线相交于O,且∠BOC=130°,则∠A=( )
| A、50° | B、60° |
| C、80° | D、100° |
已知0<x<3,化简
-
的结果是( )
| (2x+1)2 |
| x2-10x+25 |
| A、3x-4 | B、x-4 |
| C、3x+6 | D、-x+6 |
下列方程是一元二次方程的是( )
| A、x+1=3 |
| B、x2=0 |
| C、4x2-2x+1=4x2 |
| D、x2+y=0 |
 如图,AD⊥AB,AD=AB,CE=CD,BE⊥BD,试判断线段CD和线段CE的位置关系,并证明.
如图,AD⊥AB,AD=AB,CE=CD,BE⊥BD,试判断线段CD和线段CE的位置关系,并证明.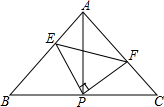 如图所示,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E,F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),给出以下五个结论:①AE=CF;②△EPF是等腰直角三角形;③S四边形AEPF=
如图所示,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E,F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),给出以下五个结论:①AE=CF;②△EPF是等腰直角三角形;③S四边形AEPF= 如图,AB是⊙O的直径,C是BA延长线上一点,点D在☉O上,且CD=OA,CD的延长线交⊙O于点E.若∠C=20°,则∠BOE的度数是
如图,AB是⊙O的直径,C是BA延长线上一点,点D在☉O上,且CD=OA,CD的延长线交⊙O于点E.若∠C=20°,则∠BOE的度数是