题目内容
15.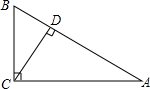 如图,在△ABC中,∠ACB=90°,CD⊥AB,BD=2,AD=4,求AC和cos∠BCD.
如图,在△ABC中,∠ACB=90°,CD⊥AB,BD=2,AD=4,求AC和cos∠BCD.
分析 首先证明△ACB∽△ADC,进而可得$\frac{AD}{AC}$=$\frac{AC}{AB}$,然后可得AC的值,再证明∠BCD=∠A,从而得到cos∠BCD=cos∠A,然后根据余弦定理可得答案.
解答 解:∵CD⊥AB,
∴∠ADC=90°,
∵∠ACB=90°,
∴∠ADC=∠ACB,
∵∠A=∠A,
∴△ACB∽△ADC,
∴$\frac{AD}{AC}$=$\frac{AC}{AB}$,
∴AC2=AD•AB=4×6=24,
∴AC=2$\sqrt{6}$,
∵∠ACB=90°,
∴∠A+∠B=90°,
∵∠BDC=90°,
∴∠B+∠BCD=90°,
∴∠BCD=∠A,
∴cos∠BCD=cos∠A=$\frac{AD}{AC}$=$\frac{4}{2\sqrt{6}}$=$\frac{\sqrt{6}}{3}$.
点评 此题主要考查了解直角三角形,以及相似三角形的判定和性质,关键是正确证明出△ACB∽△ADC.

练习册系列答案
相关题目
6.已知$\frac{x}{y}$=$\frac{1}{3}$,那么$\frac{x+y}{x-y}$的值为( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
10.抛物线y=(x+1)2-1的顶点坐标为( )
| A. | (-1,-1) | B. | (1,-1) | C. | (-1,1) | D. | (1,1) |
4. 如图,在一密闭的圆柱形玻璃杯中装一半的水,水平放置时,水面的形状是( )
如图,在一密闭的圆柱形玻璃杯中装一半的水,水平放置时,水面的形状是( )
 如图,在一密闭的圆柱形玻璃杯中装一半的水,水平放置时,水面的形状是( )
如图,在一密闭的圆柱形玻璃杯中装一半的水,水平放置时,水面的形状是( )| A. | 圆 | B. | 长方形 | C. | 椭圆 | D. | 平行四边形 |

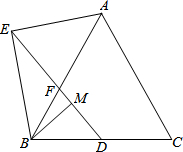 已知:在等边△ABC中,点D为BC边的中点,点F在AB上,连结DF并延长到点E,使∠BAE=∠BDF,点M在线段DF上,且∠ABE=∠DBM.
已知:在等边△ABC中,点D为BC边的中点,点F在AB上,连结DF并延长到点E,使∠BAE=∠BDF,点M在线段DF上,且∠ABE=∠DBM.