题目内容
20.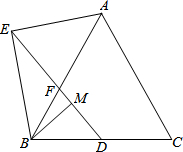 已知:在等边△ABC中,点D为BC边的中点,点F在AB上,连结DF并延长到点E,使∠BAE=∠BDF,点M在线段DF上,且∠ABE=∠DBM.
已知:在等边△ABC中,点D为BC边的中点,点F在AB上,连结DF并延长到点E,使∠BAE=∠BDF,点M在线段DF上,且∠ABE=∠DBM.(1)如图,线段AE、MD之间的数量关系为AE=2MD;请证明你的结论.
(2)在(1)的条件下,延长BM到P,使MP=BM,连接CP,若AB=7,AE=2$\sqrt{7}$,求tan∠BCP的值.
分析 (1)根据等边三角形的性质得到∠ABC=60°及△DBM∽△ABE,根据相似三角形的对应边成比例,即可求得MD=$\frac{1}{2}$AE,继而可得AE=2MD;
(2)由于△ABE∽△DBM,相似比为2,故有EB=2BM,由题意知得△BEP为等边三角形,有EM⊥BP,∠BMD=∠AEB=90°,在Rt△AEB中求得AE、AB、tan∠EAB的值,由D为BC中点,M为BP中点,得DM∥PC,求得tan∠PCB的值.
解答  解:(1)如图1,线段AE、MD之间的数量关系为 AE=2MD;
解:(1)如图1,线段AE、MD之间的数量关系为 AE=2MD;
理由:连接AD,
∵∠BAE=∠BDM,∠ABE=∠DBM,
∴△ABE∽△DBM,
∴$\frac{DM}{AE}=\frac{DB}{AB}$=cos∠ABC=cos60°=$\frac{1}{2}$,
∴MD=$\frac{1}{2}$AE,
∴AE=2MD;
(2)如图2,连接AD,EP,过N作NH⊥AC,垂足为H,连接NH, ∵AB=AC,∠ABC=60°,
∵AB=AC,∠ABC=60°,
∴△ABC是等边三角形,
又∵D为BC的中点,
∴AD⊥BC,∠DAC=30°,BD=DC=$\frac{1}{2}$AB,
∵∠BAE=∠BDM,∠ABE=∠DBM,
∴△ABE∽△DBM,
∴$\frac{BE}{BM}=\frac{AB}{DB}$=2,∠AEB=∠DMB,
∴EB=2BM,
又∵BM=MP,
∴EB=BP,
∵∠EBM=∠EBA+∠ABM=∠MBD+∠ABM=∠ABC=60°,
∴△BEP为等边三角形,
∴EM⊥BP,
∴∠BMD=90°,
∴∠AEB=90°,
在Rt△AEB中,AE=2$\sqrt{7}$,AB=7,
∴BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=$\sqrt{21}$,
∴tan∠EAB=$\frac{BE}{AE}$=$\frac{\sqrt{3}}{2}$,
∵D为BC中点,M为BP中点,
∴DM∥PC,
∴∠MDB=∠PCB,
∴∠EAB=∠PCB,
∴tan∠PCB=$\frac{\sqrt{3}}{2}$.
点评 此题考查了相似三角形的判定与性质,等边三角形的判定与性质,直角三角形的性质,以及锐角三角函数的定义,通过作辅助线使线段与线段的关系得到明确.本题的计算量大,难度适中.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案| A. | 7℃ | B. | 5℃ | C. | -5℃ | D. | -7℃ |
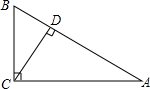 如图,在△ABC中,∠ACB=90°,CD⊥AB,BD=2,AD=4,求AC和cos∠BCD.
如图,在△ABC中,∠ACB=90°,CD⊥AB,BD=2,AD=4,求AC和cos∠BCD. 在正方形的四个顶点处标上“和谐稠州”四个字,将正方形放置在数轴上,其中“稠”“州”对应的数分别为-2和-1,现将正方形绕着顶点顺时针方向在数轴上向右无滑动的翻滚,例如第一次翻滚后“和“所对应的数为0,则连续翻滚后数轴上数2015对应的字是( )
在正方形的四个顶点处标上“和谐稠州”四个字,将正方形放置在数轴上,其中“稠”“州”对应的数分别为-2和-1,现将正方形绕着顶点顺时针方向在数轴上向右无滑动的翻滚,例如第一次翻滚后“和“所对应的数为0,则连续翻滚后数轴上数2015对应的字是( )