题目内容
7.【阅读思考】,小聪在复习过程中,发现可以用“两数的差”来表示“数轴上两点间的距离”.探索过程如下:结合数轴,解答下面的问题:
(1)数轴上表示2和5的两点之间的距离是5-2=3,数轴上表示-2和-5的两点之间的距离是3,数轴上表示1和-3的两点之间的距离是4;
【尝试应用】:
(2)把一条数轴在数m处对折,使表示-14和2014两数的点恰好互相重合,则m=1000.
【问题解决】:
(3)请你借助“数轴上的距离”帮助小红解决下列问题:
一天,小红去问曾当过数学老师现在退休在家的爷爷的年龄,爷爷说:“我若是你现在这么大,你还要40年才出生;你若是我现在这么大,我已经125岁,是老寿星了,哈哈!”,请问爷爷现在70岁.
分析 (1)根据两点间的距离,即可解答;
(2)根据数轴的对称性,即可解答;
(3)设小红x岁,爷爷y岁,根据题意求出x与y的值即可.
解答 解:(1)数轴上表示2和5的两点之间的距离是5-2=3,数轴上表示-2和-5的两点之间的距离是-2-(-5)=3,数轴上表示1和-3的两点之间的距离是1-(-3)=4,故答案为:3,4;
(2)∵把一条数轴在数m处对折,使表示-14和2014两数的点恰好互相重合,
∴m-(-14)=2014-m
∴m=1000,
故答案为:1000.
(3)设小红x岁,爷爷y岁,
根据题意得:y-x=40+x①;y-x=125-y②,
联立①②,解得:x=15,y=70,
则现在小红15岁,爷爷70岁.
故答案为:70.
点评 此题考查了数轴,弄清题中阅读材料中的意思,得出数轴上表示A与B两点间的距离AB=|a-b|是解决本题的关键.

练习册系列答案
相关题目
17.已知点P1(a,2013)和P2(-2012,b)关于原点对称,则(a+b)2015的值为( )
| A. | 1 | B. | -1 | C. | 72015 | D. | -72015 |
18.某超市在“元旦”促销期间规定:超市内所有商品按标价的80%出售,同时当顾客在消费满一定金额后,按如下方案获得相应金额的奖券:
根据上述促销方法知道,顾客在超市内购物可以获得双重优惠,即顾客在超市内购物获得的优惠额=商品的折扣+相应的奖券金额,例如:购买标价为440元的商品,则消费金额为:440×80%=352元,获得的优惠额为:440×(l-80%)+40=128元.
(1)若购买一件标价为800元的商品,则消费金额为640元,获得的优惠额是290元;
(2)若购买一件商品的消费金额a在450≤a<800之间,请用含a的代数式表示优惠额;
(3)某顾客购买一件商品的消费金额在100元与800元之间(含100元,不含800元),她能否获得150元的优惠额?若能,求出该商品的消费金额.
| 消费金额a(元)的范围 | 100≤a<400 | 400≤a<600 | 600≤a<800 |
| 获得奖券金额(元) | 40 | 100 | 130 |
(1)若购买一件标价为800元的商品,则消费金额为640元,获得的优惠额是290元;
(2)若购买一件商品的消费金额a在450≤a<800之间,请用含a的代数式表示优惠额;
(3)某顾客购买一件商品的消费金额在100元与800元之间(含100元,不含800元),她能否获得150元的优惠额?若能,求出该商品的消费金额.
2.已知实数a,b满足|a-7|+$\sqrt{b-11}$=0,则以a,b的值为两边长的等腰三角形的周长是( )
| A. | 18 | B. | 25 | C. | 29 | D. | 25或29 |
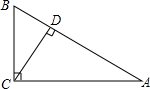 如图,在△ABC中,∠ACB=90°,CD⊥AB,BD=2,AD=4,求AC和cos∠BCD.
如图,在△ABC中,∠ACB=90°,CD⊥AB,BD=2,AD=4,求AC和cos∠BCD.