题目内容
18.先化简,再求值:($\frac{3x+4}{{x}^{2}-1}$-$\frac{2}{x-1}$)÷$\frac{x+2}{{x}^{2}-2x+1}$,其中x=tan45°+2cos60°.分析 先将分式和x化简,然后将x的值代入即可求出答案.
解答 解:原式=[($\frac{3x+4}{(x+1)(x-1)}$-$\frac{2(x+1)}{(x+1)(x-1)}$)]•$\frac{(x-1)^{2}}{x+2}$
=$\frac{x+2}{(x+1)(x-1)}-\frac{(x-1)^{2}}{x+2}$
=$\frac{x-1}{x+1}$
∵x=tan45°+2cos60°=1+2×$\frac{1}{2}$=2,
∴原式=$\frac{2-1}{2+1}$=$\frac{1}{3}$
点评 本题考查分式的运算,解题的关键是将分式和x进行化简,本题属于基础题型.

练习册系列答案
相关题目
8.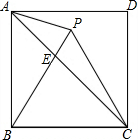 如图,点P在正方形ABCD内,△PBC是正三角形,AC与PB相交于点B,有以下结论:
如图,点P在正方形ABCD内,△PBC是正三角形,AC与PB相交于点B,有以下结论:
①∠ACP=15°;
②△APE是等腰三角形;
③AE2=PE•AB;
④△APC的面积为S1,正方形ABCD的面积为S2,则S1:S2=1:4.
其中正确的个数为 ( )
 如图,点P在正方形ABCD内,△PBC是正三角形,AC与PB相交于点B,有以下结论:
如图,点P在正方形ABCD内,△PBC是正三角形,AC与PB相交于点B,有以下结论:①∠ACP=15°;
②△APE是等腰三角形;
③AE2=PE•AB;
④△APC的面积为S1,正方形ABCD的面积为S2,则S1:S2=1:4.
其中正确的个数为 ( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
13.2016年,南平市生产总值(GDP)完成145 774 000 000元,将145 774 000 000用科学记数法表示为( )
| A. | 145 774×106 | B. | 14 577.4×107 | C. | 1.457 74×1011 | D. | 0.145 774×1012 |
3.若样本x1+1,x2+1,x3+1…,xn+1的平均数为10,方差为2,则对于样本x1+2,x2+2,x3+2…,xn+2的平均数和方差分别是( )
| A. | 10,2 | B. | 11,3 | C. | 11,2 | D. | 12,4 |