题目内容
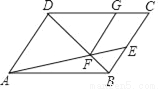
已知:如图,在平行四边形ABCD中,AD=2,点E是边BC的中点,AE、BD相交于点F,过点F作FG∥BC,交边DC于点G.
(1)求FG的长;
(2)设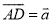 ,
, 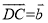 ,用
,用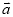 、
、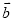 的线性组合表示
的线性组合表示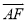 .
.
练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
题目内容
已知:如图,在平行四边形ABCD中,AD=2,点E是边BC的中点,AE、BD相交于点F,过点F作FG∥BC,交边DC于点G.
(1)求FG的长;
(2)设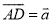 ,
, 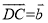 ,用
,用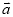 、
、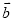 的线性组合表示
的线性组合表示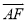 .
.

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案