题目内容
2．半径为8的圆内，垂直平分半径的弦长是8$\sqrt{3}$．分析 首先作出图形，连接OA，在直角△OAD中根据勾股定理即可求得AD的长，则弦AB=2AD．
解答 解：连接OA，如图所示：
在直角△OAD中，
∵OA=4cm，OD=2cm，
∴AD=$\sqrt{O{A}^{2}-O{D}^{2}}$=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$，
∵OC⊥AB，
∴AB=2AD=8$\sqrt{3}$．
故答案为：8$\sqrt{3}$．
点评 本题主要考查了垂径定理，弦、半径、弦心距之间的计算一般可以转化为直角三角形中的计算，运用勾股定理求出AD是解决问题的关键．
练习册系列答案
阅读快车系列答案
相关题目
12．某市规定如下用水收费标准：每户每月用水不超过6立方米时，水费按每立方米a元收费；超过6立方米时，不超过的部分每立方米仍按a元收费，超过的部分每立方米按b元收费．该市某户今年3、4月份的用水量和水费如下表所示：
（1）求出a与b的值；
（2）求当用户用水为x立方米时的水费（用含x的代数式表示）；
（3）某用户某月交水费39元，这个月该用户用水多少立方米？
| 月份 | 用水量（立方米） | 水费（元） |
| 3 | 5 | 7.5 |
| 4 | 9 | 27 |
（2）求当用户用水为x立方米时的水费（用含x的代数式表示）；
（3）某用户某月交水费39元，这个月该用户用水多少立方米？
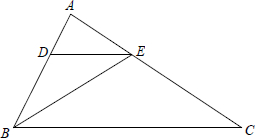如图△ABC中，BE平分∠ABC，DE∥BC，若DE=2AD，AE=2，那么EC=4．