题目内容
10．口袋中有4个白球和若干黑球，它们只有颜色不同，已知从中随机摸出一个白球的概率为$\frac{1}{3}$，则口袋中的黑球个数为8．分析 根据白球的个数和摸出一个白球的概率，求出总球的个数，再减去白球的个数，即可得出口袋中黑球的个数．
解答 解：球的总个数为：4÷$\frac{1}{3}$=12（个），
黑球的个数：12-4=8（个）．
答：口袋中黑球的个数为8个；
故答案为：8．
点评 此题考查了概率公式，用到的知识点为：可能性=所求情况数与总情况数之比．
练习册系列答案
相关题目
20．下列函数中，在x＞0时，y随x增大而减小的是（ ）
| A． | y=2x-1 | B． | y=-$\frac{1}{2}$x2+7x+$\frac{11}{2}$ | C． | y=-$\frac{2}{x}$ | D． | y=$\frac{2015}{x}$ |
5．已知二次函数y=2（x+a）2+b的顶点坐标为（2，-3），则a，b的值分别为（ ）
| A． | 2，-3 | B． | -2，-3 | C． | 2，3 | D． | -2，3 |
如图，AB是圆O的直径，C，D分别为圆周上直径AB两侧的点，若∠ADC=3∠CAB．求∠CAB的度数．
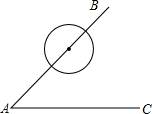如图所示，∠BAC=60°，O是射线AB上一点，以O为圆心，$\frac{1}{2}$OA的长为半径的⊙O，将AC绕点A逆时针旋转30°时，AC与⊙O相切．
如图，在△ABC中，D是BC边中点，DE⊥DF交AB于点E，DF交AC于点F．若CF2+BE2=EF2，求证：AB2+AC2=BC2．