题目内容
已知(x2-5x+3)(x3+mx+n)的计算结果中不含x3和x2项,求m,n的值.
考点:多项式乘多项式
专题:
分析:首先利用多项式乘以多项式运算法则将多项式展开,进而利用x3和x2项的系数为0,求出即可.
解答:解:(x2-5x+3)(x3+mx+n)
=x5+mx3+nx2-5x4-5mx2-5nx+3x3+3mx+3n
=x5+(m+3)x3+(n-5m)x2-5x4-5nx+3mx+3n.
∵(x2-5x+3)(x3+mx+n)的计算结果中不含x3和x2项,
∴m+3=0,n-5m=0,
解得:m=-3,n-15.
=x5+mx3+nx2-5x4-5mx2-5nx+3x3+3mx+3n
=x5+(m+3)x3+(n-5m)x2-5x4-5nx+3mx+3n.
∵(x2-5x+3)(x3+mx+n)的计算结果中不含x3和x2项,
∴m+3=0,n-5m=0,
解得:m=-3,n-15.
点评:此题主要考查了多项式乘以多项式运算,正确利用运算法则求出是解题关键.

练习册系列答案
相关题目
若|x-
|+|2y+1|=0,则x2+y2的值是( )
| 1 |
| 2 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
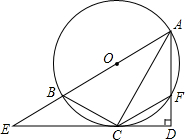 如图,Rt△ADE中,∠D=90°,点O为斜边上一点,以AB为直径的⊙O交ED于点C,连接CA、CB、CF,
如图,Rt△ADE中,∠D=90°,点O为斜边上一点,以AB为直径的⊙O交ED于点C,连接CA、CB、CF,
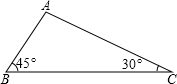 如图所示,△ABC中,∠A=30°,∠B=45°,AC=2,求AB及△ABC的面积.
如图所示,△ABC中,∠A=30°,∠B=45°,AC=2,求AB及△ABC的面积.