题目内容
12.解下列方程组(1)$\left\{\begin{array}{l}{x=2y}\\{3x-2y=8}\end{array}\right.$
(2)$\left\{\begin{array}{l}{x+\frac{1}{4}y=9}\\{\frac{1}{5}x+y=17}\end{array}\right.$.
分析 (1)方程组利用代入消元法求出解即可;
(2)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{x=2y①}\\{3x-2y=8②}\end{array}\right.$,
把①代入②得:6y-2y=8,即y=2,
把y=2代入①得:x=4,
则方程组的解为$\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$;
(2)方程组整理得:$\left\{\begin{array}{l}{4x+y=36①}\\{x+5y=85②}\end{array}\right.$,
①×5-②得:19x=85,即x=5,
把x=5代入②得:y=16,
则方程组的解为$\left\{\begin{array}{l}{x=5}\\{y=16}\end{array}\right.$.
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
3.下列各式成立的是( )
| A. | -5(x-y)=-5x+5y | B. | -2(-a+c)=-2a-2c | C. | 3-(x+y+z)=-x+y-z | D. | 3(a+2b)=3a+2b |
4.计算(-3)+(-2)的结果等于( )
| A. | -5 | B. | 5 | C. | -1 | D. | 1 |
1.在平面直角坐标系中,下面的点在第三象限的是( )
| A. | (1,2) | B. | (2,-1) | C. | (-2,4) | D. | (-3,-3) |
 如图,AB∥CD,∠B=72°,∠D=42°,求∠F的度数.
如图,AB∥CD,∠B=72°,∠D=42°,求∠F的度数. (1)如图在平行四边形ABCD中,PQ、MN分别平行DC、AD、PQ、MN交于O点,其中S四边形AMOP=3,S四边形MBQO=4,S四边形NCQO=10,则△DMQ的面积=$\frac{17}{2}$.
(1)如图在平行四边形ABCD中,PQ、MN分别平行DC、AD、PQ、MN交于O点,其中S四边形AMOP=3,S四边形MBQO=4,S四边形NCQO=10,则△DMQ的面积=$\frac{17}{2}$.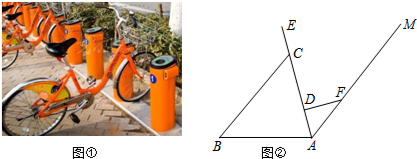
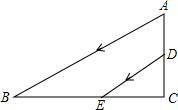 如图,AB、DE是一束平行的阳关从教室的窗口AD射入的平面示意图,且阳光AB与地面BC的夹角为30°,阳光在室内地面的影长BE=2$\sqrt{3}$m,窗口的下檐到教室地面的距离DC=1.2m.求窗顶到地面的距离AC的长.
如图,AB、DE是一束平行的阳关从教室的窗口AD射入的平面示意图,且阳光AB与地面BC的夹角为30°,阳光在室内地面的影长BE=2$\sqrt{3}$m,窗口的下檐到教室地面的距离DC=1.2m.求窗顶到地面的距离AC的长.