题目内容
9. 如图,在△ABC中,∠BAC:∠B:∠C=3:1:1,AD,AE将∠BAC三等分,点D,E在BC上.
如图,在△ABC中,∠BAC:∠B:∠C=3:1:1,AD,AE将∠BAC三等分,点D,E在BC上.(1)求∠ADE的度数;
(2)写出图中所有有两个内角相等的三角形.
分析 ( )根据已知条件和三角形的内角和得到∠BAC=120°,∠B=30°,∠C=30°,由于AD,AE将∠BAC三等分,于是求得∠BAD=∠DAE=∠EAC=36°;
(2)根据外角的性质和三角形的内角和得到∠ADE=∠AED=∠BAE=∠CAD=72°,于是得到结论.
解答 解:(1)∵∠BAC:∠B:∠C=3:1:1,∠BAC+∠B+∠C=180°,
∴∠BAC=108°,∠B=36°,∠C=36°,
∵AD,AE将∠BAC三等分,
∴∠BAD=∠DAE=∠EAC=36°;
(2)∵∠BAD=∠DAE=∠EAC=36°,
∴∠ADE=∠AED=∠BAE=∠CAD=72°,
∴AD=BD,AD=AE,AE=CE,AB=AC,AB=BE,AC=CD,
∴△ABD,△ADE,△AEC,△ABC,△ABE,△ACD是等腰三角形,
∴图中所有有两个内角相等的三角形等腰三角形是∴△ABD,△ADE,△AEC,△ABC,△ABE,△ACD.
点评 本题考查了三角形内角和定理、等腰三角形的判定;熟练掌握三角形内角和定理,解题的关键是求出每个角的度数.

练习册系列答案
相关题目
13.下列哪个方程组的解组成的有序数对是一次函数y=2-x和y=3x+2的图象的交点坐标( )
| A. | $\left\{\begin{array}{l}{y+x=2}\\{y-3x=-2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{y+x=2}\\{y-3x=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{y+x=-2}\\{y-3x=-2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{y+x=-2}\\{y-3x=2}\end{array}\right.$ |
4.如图所示是甲、乙两所学校学生喜欢不同书籍的统计图(A:科幻,B:侦探,C:文学,D:艺术):根据统计图,下列对两校喜欢文学类书籍的人数占全校总人数的百分比做出的判断中,正确的是( )


| A. | 甲校比乙校大 | B. | 乙校比甲校大 | C. | 甲、乙两校一样大 | D. | 无法判断 |
18.张大爷离家出门散步,他先向正东走了80m,接着又向正南走了150m,此时他离家的距离为( )
| A. | 200m | B. | 160 m | C. | 170 m | D. | 180 m |
19. 如图,在△ABC中,D在BC上,若AD=BD,AB=AC=CD,则∠ABC的度数是( )
如图,在△ABC中,D在BC上,若AD=BD,AB=AC=CD,则∠ABC的度数是( )
 如图,在△ABC中,D在BC上,若AD=BD,AB=AC=CD,则∠ABC的度数是( )
如图,在△ABC中,D在BC上,若AD=BD,AB=AC=CD,则∠ABC的度数是( )| A. | 30° | B. | 35° | C. | 36° | D. | 60° |
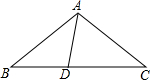 如图,已知,D为△ABC中BC边上一点,∠B=∠C=∠DAB,且∠ADC=∠DAC,求∠BAC的度数.
如图,已知,D为△ABC中BC边上一点,∠B=∠C=∠DAB,且∠ADC=∠DAC,求∠BAC的度数.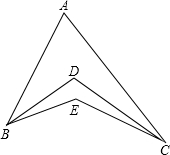 如图,∠ABE、∠ACE的三等分线(分别靠近BE、CE)交于点D,则∠E、∠D、∠A之间的数量关系为2∠A+∠D=3∠E.
如图,∠ABE、∠ACE的三等分线(分别靠近BE、CE)交于点D,则∠E、∠D、∠A之间的数量关系为2∠A+∠D=3∠E.