题目内容
19. 如图,在△ABC中,D在BC上,若AD=BD,AB=AC=CD,则∠ABC的度数是( )
如图,在△ABC中,D在BC上,若AD=BD,AB=AC=CD,则∠ABC的度数是( )| A. | 30° | B. | 35° | C. | 36° | D. | 60° |
分析 AB=AC可得∠B=∠C,CD=DA可得∠ADB=2∠C=2∠B,BA=BD,可得∠BDA=∠BAD=2∠B,在△ABD中利用三角形内角和定理可求出∠B.
解答 解:∵AB=AC,
∴∠B=∠C,
∵CD=DA,
∴∠C=∠DAC,
∵BA=BD,
∴∠BDA=∠BAD=2∠C=2∠B,
又∵∠B+∠BAD+∠BDA=180°,
∴5∠B=180°,
∴∠B=36°,
故选C.
点评 本题主要考查等腰三角形的性质,掌握等边对等角是解题的关键,注意三角形内角和定理和方程思想的应用.

练习册系列答案
相关题目
14.已知a是两位数,b是一位数,把b接写在a的后面,就成为一个三位数.这个三位数可表示成( )
| A. | 10a+b | B. | ab | C. | 100a+b | D. | a+10b |
8.以下列各组数据为三角形三边,不能构成三角形的是( )
| A. | 4,8,7 | B. | 3,4,7 | C. | 2,3,4 | D. | 13,12,5 |
 如图,在△ABC中,∠BAC:∠B:∠C=3:1:1,AD,AE将∠BAC三等分,点D,E在BC上.
如图,在△ABC中,∠BAC:∠B:∠C=3:1:1,AD,AE将∠BAC三等分,点D,E在BC上.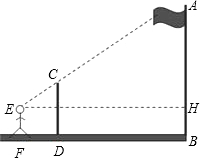 为测量操场上悬挂国旗的旗杆的高度,设计的测量方案如图所示:标杆高度CD=3m,标杆与旗杆的水平距离BD=15m,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,E,C,A三点共线,求旗杆AB的高度.
为测量操场上悬挂国旗的旗杆的高度,设计的测量方案如图所示:标杆高度CD=3m,标杆与旗杆的水平距离BD=15m,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,E,C,A三点共线,求旗杆AB的高度. 已知等边三角形ABC的边长为6cm
已知等边三角形ABC的边长为6cm