题目内容
17.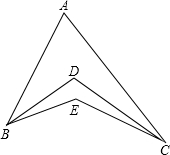 如图,∠ABE、∠ACE的三等分线(分别靠近BE、CE)交于点D,则∠E、∠D、∠A之间的数量关系为2∠A+∠D=3∠E.
如图,∠ABE、∠ACE的三等分线(分别靠近BE、CE)交于点D,则∠E、∠D、∠A之间的数量关系为2∠A+∠D=3∠E.
分析 根据∠ACE=$\frac{1}{3}$∠ACD,∠ABE=$\frac{1}{3}$∠ABD,求得∠ACE=$\frac{1}{2}$∠ECD,∠ABE=$\frac{1}{2}$∠EBD,然后根据三角形的内角和即可得到结论.
解答 解:2∠A+∠D=3∠E.连接BC.如图所示: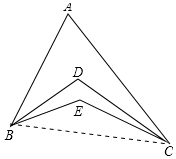
∵∠ACE=$\frac{1}{3}$∠ACD,∠ABE=$\frac{1}{3}$∠ABD,
∴∠ACE=$\frac{1}{2}$∠ECD,∠ABE=$\frac{1}{2}$∠EBD,
又∵∠CDB=180°-∠DCB-∠DBC,
∠CEB=180°-∠ECD-∠EBD-∠DCB-∠DBC=180°-2∠ACE-2∠ABE-∠DCB-∠DBC,
∠A=180°-∠ACE-∠ABE-∠ECD-∠EBD-∠DCB-∠DBC=180°-3∠ACE-3∠ABE-∠DCB-∠DBC,
∴2∠A+∠D=3∠E.
故答案为:2∠A+∠D=3∠E.
点评 本题考查三角形的角平分线和三角形外角和内角的关系,灵活的运用相关知识解答本题.

练习册系列答案
相关题目
12. 如图,点D、E分别是△ABC的边AB和AC的中点,已知BC=2,则DE的长为( )
如图,点D、E分别是△ABC的边AB和AC的中点,已知BC=2,则DE的长为( )
 如图,点D、E分别是△ABC的边AB和AC的中点,已知BC=2,则DE的长为( )
如图,点D、E分别是△ABC的边AB和AC的中点,已知BC=2,则DE的长为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
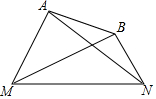 如图,点A、B是线段MN上方两点.AN与BM相交于点C,且∠AMN=∠BNM=60°,∠MAN+∠MBN=180°.
如图,点A、B是线段MN上方两点.AN与BM相交于点C,且∠AMN=∠BNM=60°,∠MAN+∠MBN=180°. 如图,在△ABC中,AD⊥BC,垂足为D,E为AC上一点,BE交AD于点F,且BF=AC,FD=CD,AD=4,则AB=4$\sqrt{2}$.
如图,在△ABC中,AD⊥BC,垂足为D,E为AC上一点,BE交AD于点F,且BF=AC,FD=CD,AD=4,则AB=4$\sqrt{2}$. 如图,在△ABC中,∠BAC:∠B:∠C=3:1:1,AD,AE将∠BAC三等分,点D,E在BC上.
如图,在△ABC中,∠BAC:∠B:∠C=3:1:1,AD,AE将∠BAC三等分,点D,E在BC上.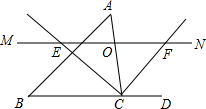 如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.求证:OE=OF.
如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.求证:OE=OF.