题目内容
12.若关于x的方程(k-1)x2+2x-2=0有实数根,则k的取值范围是( )| A. | k$≥\frac{1}{2}$且k≠1 | B. | k$≥\frac{1}{2}$ | C. | k$>\frac{1}{2}$ | D. | k$>\frac{1}{2}$且k≠1 |
分析 当k-1=0时,原方程为一元一次方程,方程有解;当k-1≠0时,由方程有解结合根的判别式即可得出△=8k-4≥0,解之即可得出k的取值范围.综上即可得出结论.
解答 解:当k-1=0即k=1时,原方程为2x-2=0,
解得:x=1,
∴当k=1时,原方程有实数根;
当k-1≠0即k≠1时,△=22-4(k-1)×(-2)=8k-4≥0,
解得:k≥$\frac{1}{2}$.
故选B.
点评 本题考查了根的判别式,分k-1=0和k-1≠0两种情况考虑是解题的关键.

练习册系列答案
相关题目
17.如表是某次篮球联赛积分的一部分
(1)请问胜一场积多少分?负一场积多少分?
(2)某队的负场总积分是胜场总积分的n倍,n为正整数,求n的值.
(注意:本题只能用一元一次方程求解,否则不给分).
| 球队 | 比赛现场 | 胜场 | 负场 | 积分 |
| 前进 | 14 | 10 | 4 | 24 |
| 光明 | 14 | 9 | 5 | 23 |
| 远大 | 14 | 7 | 7 | 21 |
| 卫星 | 14 | 4 | 10 | 18 |
| 备注:积分=胜场积分+负场积分 | ||||
(2)某队的负场总积分是胜场总积分的n倍,n为正整数,求n的值.
(注意:本题只能用一元一次方程求解,否则不给分).
4. 如图,用图中所示的扇形纸片围成一个圆锥,已知扇形的半径为5,弧长是6π,那么围成的圆锥的高度是( )
如图,用图中所示的扇形纸片围成一个圆锥,已知扇形的半径为5,弧长是6π,那么围成的圆锥的高度是( )
 如图,用图中所示的扇形纸片围成一个圆锥,已知扇形的半径为5,弧长是6π,那么围成的圆锥的高度是( )
如图,用图中所示的扇形纸片围成一个圆锥,已知扇形的半径为5,弧长是6π,那么围成的圆锥的高度是( )| A. | $\sqrt{11}$ | B. | 5 | C. | 4 | D. | 3 |
1.比-2小的数是( )
| A. | -4 | B. | $\frac{1}{2}$ | C. | 0 | D. | -1 |
2.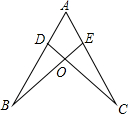 如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( )
如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( )
 如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( )
如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( )| A. | ∠B=∠C | B. | BE=CD | C. | BD=CE | D. | AD=AE |
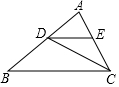 如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,∠BDC=∠CED,如果DE=4,CD=6,那么AD:AE等于3:2.
如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,∠BDC=∠CED,如果DE=4,CD=6,那么AD:AE等于3:2.