题目内容
4．
如图，用图中所示的扇形纸片围成一个圆锥，已知扇形的半径为5，弧长是6π，那么围成的圆锥的高度是（ ）| A． | $\sqrt{11}$ | B． | 5 | C． | 4 | D． | 3 |
分析 已知弧长即已知围成的圆锥的底面的周长是6πcm，这样就求出底面圆的半径．扇形的半径为5cm就是圆锥的母线长是5cm．就可以根据勾股定理求出圆锥的高．
解答 解：设底面圆的半径是r，则2πr=6π，
∴r=3，
∴圆锥的高=$\sqrt{{5}^{2}-{3}^{2}}$=4．
故选C．
点评 本题考查的是圆锥的计算．本题利用了勾股定理，圆的周长公式求解．
练习册系列答案
一本好题口算题卡系列答案
相关题目
如图，已知AD∥BE∥CF，它们依次交直线l1、l2于点A、B、C和点D、E、F．如果AB=6，BC=10，那么$\frac{DE}{DF}$的值是$\frac{3}{8}$．
12．若关于x的方程（k-1）x2+2x-2=0有实数根，则k的取值范围是（ ）
| A． | k$≥\frac{1}{2}$且k≠1 | B． | k$≥\frac{1}{2}$ | C． | k$＞\frac{1}{2}$ | D． | k$＞\frac{1}{2}$且k≠1 |
19．若点P在线段AB上，PB=4，PA=$\frac{1}{2}$PB，则AB的长度是（ ）
| A． | 3 | B． | 6 | C． | 12 | D． | 6或12 |
9．下面不是同类项的是（ ）
| A． | -2与12 | B． | -2a2b与a2b | C． | 2m与2n | D． | -x2y2与12x2y2 |
16．化简$\frac{2}{{x}^{2}-1}$÷$\frac{1}{x-1}$的结果是（ ）
| A． | $\frac{2}{x-1}$ | B． | $\frac{2}{x}$ | C． | $\frac{2}{x+1}$ | D． | 2（x+1） |
13．
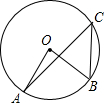如图，点A、B、C都在⊙O上，若∠AOB=76°，则∠ACB的度数为（ ）
如图，点A、B、C都在⊙O上，若∠AOB=76°，则∠ACB的度数为（ ）| A． | 19° | B． | 30° | C． | 38° | D． | 76° |
14．
有理数a，b在数轴上的位置如图，那么下列关系正确的是（ ）
有理数a，b在数轴上的位置如图，那么下列关系正确的是（ ）| A． | b＞a | B． | -a＞b | C． | |a|＞|b| | D． | a＞-b |