题目内容
20. 如图,P是△ABC斜边AB上的动点(点P不与点A、B重合),∠C=90°,∠B=45°,过点P的直线截△ABC,使所截得的三角形与△ABC相似,当$\frac{BP}{BA}$的值为$\frac{\sqrt{2}}{2}$或$\frac{1}{2}$时,所截得的三角形面积为△ABC面积的$\frac{1}{2}$.
如图,P是△ABC斜边AB上的动点(点P不与点A、B重合),∠C=90°,∠B=45°,过点P的直线截△ABC,使所截得的三角形与△ABC相似,当$\frac{BP}{BA}$的值为$\frac{\sqrt{2}}{2}$或$\frac{1}{2}$时,所截得的三角形面积为△ABC面积的$\frac{1}{2}$.
分析 由于∠PBQ=∠ABC,根据有两组角对应相等的两个三角形相似,当∠BPQ=∠A时,△BPQ∽△BAC,利用相似三角形的性质计算BP与AB;当∠BPQ=∠C时,△BPQ∽△BQP,然后利用相似三角形的性质得到BP与BC的关系,再利用等腰直角三角形的性质得到BC和AB的关系,从而得到BP和AB的关系.
解答 解:∵∠PBQ=∠ABC,
∴当∠BPQ=∠A时,△BPQ∽△BAC,此时$\frac{{S}_{△BPQ}}{{S}_{△BAC}}$=($\frac{BP}{BA}$)2=$\frac{1}{2}$,则$\frac{BP}{BA}$=$\frac{\sqrt{2}}{2}$;
当∠BPQ=∠C时,△BPQ∽△BQP,此时$\frac{{S}_{△BPQ}}{{S}_{△BAC}}$=($\frac{BP}{BC}$)2=$\frac{1}{2}$,则$\frac{BP}{BC}$=$\frac{\sqrt{2}}{2}$,而BC=$\frac{\sqrt{2}}{2}$AB,所以$\frac{BP}{BA}$=$\frac{1}{2}$,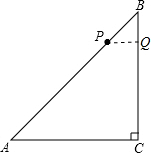
综上所述,当$\frac{BP}{BA}$的值为$\frac{\sqrt{2}}{2}$或$\frac{1}{2}$时,所截得的三角形面积为△ABC面积的$\frac{1}{2}$.
故答案为为$\frac{\sqrt{2}}{2}$或$\frac{1}{2}$.
点评 本题考查了相似三角形的判定:有两组角对应相等的两个三角形相似.也考查了等腰直角三角形的性质和分类讨论思想的运用.

练习册系列答案
相关题目
10.已知a,b是一元二次方程x2+x-1=0的两个根,则代数式2a2+b2+2a+b的值为( )
| A. | -3 | B. | -2 | C. | 2 | D. | 3 |
12.下列结论中,正确的有( )
①符号相反且绝对值相等的数互为相反数;
②一个数的绝对值越大,表示它的点在数轴上离原点越远;
③两数的差不可能等于被减数;
④绝对值等于它的相反数是负数;
⑤和为0的两数互为相反数.
①符号相反且绝对值相等的数互为相反数;
②一个数的绝对值越大,表示它的点在数轴上离原点越远;
③两数的差不可能等于被减数;
④绝对值等于它的相反数是负数;
⑤和为0的两数互为相反数.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
16.下列各组图形一定相似的是( )
| A. | 两个矩形 | B. | 两个等边三角形 | ||
| C. | 各有一角是80°的两个等腰三角形 | D. | 任意两个菱形 |