题目内容
20. 如图,等边△ABC的边长为4,点E在BA的延长线上,点D在BC边上,且ED=EC,AE=2.求BD的长.
如图,等边△ABC的边长为4,点E在BA的延长线上,点D在BC边上,且ED=EC,AE=2.求BD的长.
分析 延长BC至F点,使得CF=BD,证得△EBD≌△EFC后即可证得∠B=∠F,然后证得AC∥EF,利用平行线分线段成比例定理证得CF=EA后即可求得BD的长.
解答 解:延长BC至F点,使得CF=BD,
∵ED=EC,
∴∠EDC=∠ECD,
∴∠EDB=∠ECF,
在△EBD和△EFC中,
$\left\{\begin{array}{l}{DB=CF}\\{∠BDE=∠FCE}\\{DE=CE}\end{array}\right.$,
∴△EBD≌△EFC(SAS),
∴∠B=∠F
∵△ABC是等边三角形,
∴∠B=∠ACB,
∴∠ACB=∠F,
∴AC∥EF,
∴$\frac{AB}{AE}=\frac{BC}{CF}$,
∵BA=BC,
∴AE=CF=2,
∴BD=AE=CF=2
点评 本题考查了等腰三角形及等边三角形的性质,解题的关键是正确的作出辅助线.

练习册系列答案
相关题目
10.下列三角形纸片中能沿直线剪一刀得到等腰梯形的是( )
| A. | 一个角为50°,一个角为90°的三角形纸片 | |
| B. | 一个角为40°,一个角为120°的三角形纸片 | |
| C. | 一个角为36°,一个角为72°的三角形纸片 | |
| D. | 一个角为50°,一个角为70°的三角形纸片 |
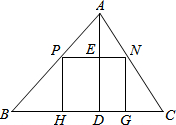 如图,三角形ABC是一块锐角三角形余料,边BC=12米,高AD=8米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?
如图,三角形ABC是一块锐角三角形余料,边BC=12米,高AD=8米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?
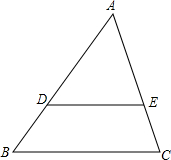 如图,若$\frac{AD}{BD}$=$\frac{AE}{EC}$,则$\frac{AD}{AB}$=$\frac{AE}{AC}$.说明理由.
如图,若$\frac{AD}{BD}$=$\frac{AE}{EC}$,则$\frac{AD}{AB}$=$\frac{AE}{AC}$.说明理由.