题目内容
15.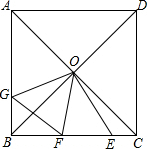 如图,在正方形ABCD中,对角线AC,BD相交于点O,点E,F为BC边上的两点,且∠EOF=45°,过点O作OE的垂线OG,交AB于点G,连接FG,下列结论:①△COE≌△BOG;②△COE≌△BOF;③CE+BF>EF;④CE2+BF2=EF2.其中正确的有( )
如图,在正方形ABCD中,对角线AC,BD相交于点O,点E,F为BC边上的两点,且∠EOF=45°,过点O作OE的垂线OG,交AB于点G,连接FG,下列结论:①△COE≌△BOG;②△COE≌△BOF;③CE+BF>EF;④CE2+BF2=EF2.其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 如图,作辅助线;首先运用正方形的性质证明OB=OC,∠OBG=∠OCE=45°;证明∠BOG=∠COE,运用ASA公理即可证明△COE≌△BOG,得到结论①正确;证明△MOE≌△COE,得到∠OME=∠OCE=45°,进而得到∠EMF=90°,运用勾股定理即可证明结论④正确,在△MEF中,ME+MF>EF,CE+BF>EF,故③正确.
解答 解:如图,作△OBF的对称△OMF,连接ME;
∵四边形ABCD为正方形,
∴OB=OC,∠OBG=∠OCE=45°,∠BOC=90°;
∵OG⊥OE,
∴∠BOG=∠COE;
在△COE与△BOG中,
$\left\{\begin{array}{l}{∠COE=∠BOG}\\{OC=OB}\\{∠OBG=∠OCE}\end{array}\right.$,
∴△COE≌△BOG(ASA),
故①正确.
设∠BOF=α,∠COE=β;
∵∠BOC=90°,∠EOF=45°,
∴α+β=90°-45°=45°;
由题意得:∠MOF=∠BOF=α,∠OMF=∠OBF=45°,
在△BOF和△MOF中,
$\left\{\begin{array}{l}{∠MOF=∠BOF}\\{∠OMF=∠OBF}\\{OF=OF}\end{array}\right.$
∴△BOF≌△MOF.
∴OM=OB,BF=MF;
则∠MOE=45°-α,OC=OM;
∵∠COE=45°-α,
∴∠MOE=∠COE;
在△MOE与△COE中,
$\left\{\begin{array}{l}{OC=OM}\\{∠COE=∠MOE}\\{OE=OE}\end{array}\right.$,
∴△MOE≌△COE(SAS),
∴ME=CE,∠OME=∠OCE=45°,
∴∠FME=90°,MF2+ME2=EF2,
即CE2+BF2=EF2,
故④正确,
∵在△MEF中,ME+MF>EF,
∴CE+BF>EF,
故③正确;
故正确为①③④.
故选:C.
点评 该题主要考查了正方形的性质、全等三角形的判定、勾股定理等几何知识点及其应用问题;解题的方法是作辅助线,将分散的条件集中;解题的关键是灵活运用正方形的性质、全等三角形的判定、勾股定理等几何知识点来分析、判断、推理或解答.

| 日 期 | 15日 | 16日 | 17日 | 18日 | 19日 | 20日 | 21日 | 22日 |
| 天然气表显示的读数/m3 | 220 | 229 | 241 | 249 | 259 | 270 | 279 | 290 |

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
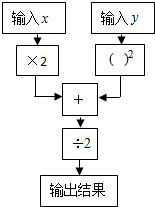 如图是一个数值转换机的示意图,当输入的x值为5,y的值为-2时,输出的结果为7.
如图是一个数值转换机的示意图,当输入的x值为5,y的值为-2时,输出的结果为7. 已知△ABC中,BC=26cm,AB、AC的垂直平分线分别交BC于E、F,则△EAF周长26cm.
已知△ABC中,BC=26cm,AB、AC的垂直平分线分别交BC于E、F,则△EAF周长26cm.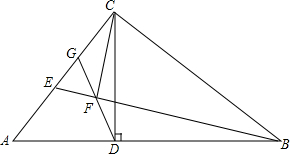 已知Rt△ABC中,∠ACB=90°,CD是高,E为AC上一点,CF⊥BE于F,FD的延长线交AC于G.
已知Rt△ABC中,∠ACB=90°,CD是高,E为AC上一点,CF⊥BE于F,FD的延长线交AC于G.