题目内容
12.在?ABCD中,对角线AC与BD相交于点O,如果△OBC的周长是59,且AD的长是28,两对角线之差是14,试分别求出两条对角线的长.分析 根据平行四边形的性质可得两对角线的和的一半是31,和已知条件建立方程求解即可.
解答 解:∵四边形ABCD是平行四边形,
∴AD=BC=28,
∵△OBC的周长为59,BC的长为28,
∴两对角线的和的一半是31,
即(BD+AC)÷2=31,
再由BD-AC=14,
解得:AC=24,BD=38,
答:平行四边形两条对角线的长分别是24,38.
点评 本题考查了平行四边形的性质,解题的关键是熟记:平行四边形的对角线互相平分.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.下列各数中,无理数是( )
| A. | $\frac{22}{7}$ | B. | $\sqrt{9}$ | C. | π | D. | $\root{3}{8}$ |
4.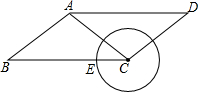 如图,已知平行四边形ABCD中,AB=5,BC=8,cosB=$\frac{4}{5}$,点E是BC边上的动点,当以CE为半径的圆C与边AD不相交时,半径CE的取值范围是( )
如图,已知平行四边形ABCD中,AB=5,BC=8,cosB=$\frac{4}{5}$,点E是BC边上的动点,当以CE为半径的圆C与边AD不相交时,半径CE的取值范围是( )
 如图,已知平行四边形ABCD中,AB=5,BC=8,cosB=$\frac{4}{5}$,点E是BC边上的动点,当以CE为半径的圆C与边AD不相交时,半径CE的取值范围是( )
如图,已知平行四边形ABCD中,AB=5,BC=8,cosB=$\frac{4}{5}$,点E是BC边上的动点,当以CE为半径的圆C与边AD不相交时,半径CE的取值范围是( )| A. | 0<CE≤8 | B. | 0<CE≤5 | C. | 0<CE<3或5<CE≤8 | D. | 3<CE≤5 |
1.已知5x-4y-7z=0,4x-3y-6z=0,则x:y:z为( )
| A. | 3:2:1 | B. | 9:4:1 | C. | 1:2:3 | D. | 1:4:9 |
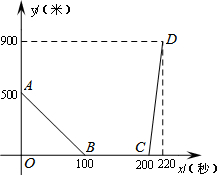 设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回.设x秒后两车间的距离为y千米,y关于x的函数关系如图所示,
设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回.设x秒后两车间的距离为y千米,y关于x的函数关系如图所示,