题目内容
6．一艘轮船以16海里/时的速度离开港口向东南方向航行，另一艘轮船在同时同地以12海里/时的速度向西南方向航行，它们离开港口3小时相距（ ）海里．| A． | 60 | B． | 30 | C． | 20 | D． | 80 |
分析 根据题意，画出图形，且东北和东南的夹角为90°，根据题目中给出的1小时后和速度可以计算AC，BC的长度，在直角△ABC中，已知AC，BC可以求得AB的长．
解答 
解：作出图形，因为东南和西南的夹角为90°，所以△ABC为直角三角形．
在Rt△ABC中，AC=16×3=48（km），
BC=12×3km=36（km）．
则AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{4{8}^{2}+3{6}^{2}}$=60（km）
故选A．
点评 本题考查了勾股定理在实际生活中的应用，本题中确定△ABC为直角三角形，并且根据勾股定理计算AB是解题的关键．
练习册系列答案
相关题目
如图，为修通铁路凿通隧道AC，量出∠C=90°，AB=5km，BC=4km，若每天凿隧道0.15km，问几天才能把隧道AC凿通？
说出如图图形中∠1和∠2的度数：55°、70°．
如图所示，图中的x的值是65°．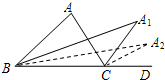
如图，已知△ABC的内角∠A=a，分别作内角∠ABC与外角∠ACD的平分线，两条平分线交于点A1，得∠A1；∠A1BC和∠A1CD的平分线交于点A2，得∠A2；…以此类推得到∠A2016，则∠A2016的度数是$\frac{α}{{2}^{2016}}$．