题目内容
16.已知$\root{3}{(x-2)^{3}}$+$\sqrt{(x-2)^{2}}$=0,则x的取值范围为( )| A. | x≤2 | B. | x<2 | C. | x≥2 | D. | x>2 |
分析 已知等式变形,利用绝对值的代数意义化简即可确定出x的范围.
解答 解:已知等式变形得:x-2+|x-2|=0,即|x-2|=2-x,
∴x-2≤0,即x≤2.
故选A
点评 此题考查了立方根,以及算术平方根,熟练掌握各自的定义是解本题的关键.

练习册系列答案
相关题目
4.下列说法:
①在△ABC中,若∠A:∠B:∠C=3:4:5,则△ABC为直角三角形;
②已知直角三角形的面积为2,两直角边的比为1:2,则斜边长的平方为10;
③在Rt△ABC中,若两边长分别为3和4,则第三边长为5;
④已知等腰三角形的面积为12,底边上的高为4,则腰长为5.
其中正确结论的序号是( )
①在△ABC中,若∠A:∠B:∠C=3:4:5,则△ABC为直角三角形;
②已知直角三角形的面积为2,两直角边的比为1:2,则斜边长的平方为10;
③在Rt△ABC中,若两边长分别为3和4,则第三边长为5;
④已知等腰三角形的面积为12,底边上的高为4,则腰长为5.
其中正确结论的序号是( )
| A. | ①②④ | B. | ①③④ | C. | ②③④ | D. | ②④ |
8.设y=ax2+bx+1(a≠0),y的最大值为1,则( )
| A. | b<0 | B. | b=0 | C. | 0<b<1 | D. | b≥1 |
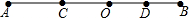 (1)如图,线段AB=4,点O是线段AB上一点,C,D分别是线段OA,OB的中点,则线段CD的长为多少?
(1)如图,线段AB=4,点O是线段AB上一点,C,D分别是线段OA,OB的中点,则线段CD的长为多少?