题目内容
6.解方程:(1)x2-10x+9=0
(2)(x-5)2=25
(3)x2+4x+1=0
(4)3x2-6x+1=0.
分析 (1)先分解因式,即可得出两个一元一次方程,求出方程的解即可;
(2)两边开方,即可得出两个一元一次方程,求出方程的解即可;
(3)求出b2-4ac的值,再代入公式求出即可;
(4)求出b2-4ac的值,再代入公式求出即可.
解答 解:(1)x2-10x+9=0,
分解因式得:(x-9)(x-1)=0,
x-1=0,x-9=0,
x1=1,x2=9;
(2)(x-5)2=25,
开方得:x-5=±5,
解得:x1=10,x2=0;
(3)x2+4x+1=0,
b2-4ac=42-4×1×1=12,
x=$\frac{-4±\sqrt{12}}{2}$,
x1=-2+$\sqrt{3}$,x2-=-2-$\sqrt{3}$;
(4)3x2-6x+1=0,
b2-4ac=(-6)2-4×3×1=24,
x=$\frac{6±\sqrt{24}}{2×3}$,
x1=$\frac{3+\sqrt{6}}{3}$,x2=$\frac{3-\sqrt{6}}{3}$.
点评 本题考查了解一元二次方程的应用,能选择适当的方法解一元二次方程是解此题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
17.下列说法正确的是( )
| A. | 2πx3的系数是2 | B. | x2y的系数是0 | C. | -2x2y的系数是2 | D. | 42y的系数是42 |
14.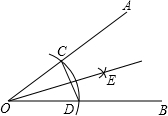 小明同学画角平分,作法如下:
小明同学画角平分,作法如下:
①以O为圆心,适当长为半径作弧,交两边于D、E
②分别以C、D为圆心,相同的长度为半径作弧,两弧交于E,
③则射线OE就是∠AOB的平分线.
小明这样做的依据是( )
 小明同学画角平分,作法如下:
小明同学画角平分,作法如下:①以O为圆心,适当长为半径作弧,交两边于D、E
②分别以C、D为圆心,相同的长度为半径作弧,两弧交于E,
③则射线OE就是∠AOB的平分线.
小明这样做的依据是( )
| A. | SAS | B. | ASA | C. | AAS | D. | SSS |
11. 已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0),对于下列结论:①b+2a=0;②abc>0;③a-b+c>0;④b2-4ac=0,其中正确的有( )
已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0),对于下列结论:①b+2a=0;②abc>0;③a-b+c>0;④b2-4ac=0,其中正确的有( )
 已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0),对于下列结论:①b+2a=0;②abc>0;③a-b+c>0;④b2-4ac=0,其中正确的有( )
已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0),对于下列结论:①b+2a=0;②abc>0;③a-b+c>0;④b2-4ac=0,其中正确的有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
15.有若干个数,第一个数记为a1,第二个数记为a2,…,第n个数记为an.若a1=$\frac{1}{2}$,从第二个数起,每个数都等于“1与它前面那个数的差的倒数”.请计算a2000( )
| A. | 2020 | B. | 2 | C. | $\frac{1}{2}$ | D. | -1 |
16.已知$\root{3}{(x-2)^{3}}$+$\sqrt{(x-2)^{2}}$=0,则x的取值范围为( )
| A. | x≤2 | B. | x<2 | C. | x≥2 | D. | x>2 |
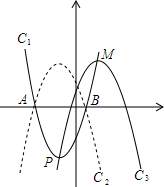 如图,已知抛物线C1:y=a(x+2)2-5的顶点为P1与x轴相交于A、B两点(点A在点B的左侧),且点B的坐标为(1,0);
如图,已知抛物线C1:y=a(x+2)2-5的顶点为P1与x轴相交于A、B两点(点A在点B的左侧),且点B的坐标为(1,0);