题目内容
大学生小张利用暑假50天在一超市勤工俭学,被安排销售一款成本为40元/件的新型商品,此类新型商品在第x天的销售量p件与销售的天数x的关系如下表:
销售单价q(元/件)与x满足:当1≤x<25时q=x+60;当25≤x≤50时q=40+
.
(1)请分析表格中销售量p与x的关系,求出销售量p与x的函数关系.
(2)求该超市销售该新商品第x天获得的利润y元关于x的函数关系式.
(3)这50天中,该超市第几天获得利润最大?最大利润为多少?
| x(天) | 1 | 2 | 3 | … | 50 |
| p(件) | 118 | 116 | 114 | … | 20 |
| 1125 |
| x |
(1)请分析表格中销售量p与x的关系,求出销售量p与x的函数关系.
(2)求该超市销售该新商品第x天获得的利润y元关于x的函数关系式.
(3)这50天中,该超市第几天获得利润最大?最大利润为多少?
考点:二次函数的应用,反比例函数的应用
专题:销售问题
分析:(1)由表格可以看出销售量p件与销售的天数x成一次函数,设出函数解析式,进一步代入求得答案即可;
(2)利用利润=售价-成本,分别求出在1≤x<25和25≤x≤50时,求得y与x的函数关系式;
(3)利用(2)中的函数解析式分别求得最大值,然后比较两者的大小得出答案即可.
(2)利用利润=售价-成本,分别求出在1≤x<25和25≤x≤50时,求得y与x的函数关系式;
(3)利用(2)中的函数解析式分别求得最大值,然后比较两者的大小得出答案即可.
解答:解:(1)设销售量p件与销售的天数x的函数解析式为p=kx+b,
代入(1,118),(2,116)得
解得
因此销售量p件与销售的天数x的函数解析式为p=-2x+120;
(2)当1≤x<25时,
y=(60+x-40)(-2x+120)
=-2x2+80x+2400,
当25≤x≤50时,
y=(40+
-40)(-2x+120)
=
-2250;
(3)当1≤x<25时,
y=-2x2+80x+2400,
=-2(x-20)2+3200,
∵-2<0,
∴当x=20时,y有最大值y1,且y1=3200;
当25≤x≤50时,
y=
-2250;
∵135000>0,
∴
随x的增大而减小,
当x=25时,
最大,
于是,x=25时,y=
-2250有最大值y2,且y2=5400-2250=3150.
∵y1>y2
∴这50天中第20天时该超市获得利润最大,最大利润为3200元.
代入(1,118),(2,116)得
|
解得
|
因此销售量p件与销售的天数x的函数解析式为p=-2x+120;
(2)当1≤x<25时,
y=(60+x-40)(-2x+120)
=-2x2+80x+2400,
当25≤x≤50时,
y=(40+
| 1125 |
| x |
=
| 135000 |
| x |
(3)当1≤x<25时,
y=-2x2+80x+2400,
=-2(x-20)2+3200,
∵-2<0,
∴当x=20时,y有最大值y1,且y1=3200;
当25≤x≤50时,
y=
| 135000 |
| x |
∵135000>0,
∴
| 135000 |
| x |
当x=25时,
| 135000 |
| x |
于是,x=25时,y=
| 135000 |
| x |
∵y1>y2
∴这50天中第20天时该超市获得利润最大,最大利润为3200元.
点评:本题主要考查二次函数的应用的知识点,解答本题的关键是熟练掌握二次函数的性质和反比例函数的性质以及最值得求法,此题难度不大.

练习册系列答案
相关题目
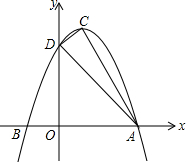 如图,抛物线y=ax2+bx+c的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D.
如图,抛物线y=ax2+bx+c的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D.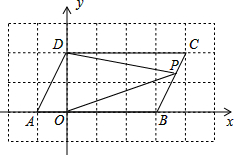 如图,在直角坐标系xOy中,A(-1,0),B(3,0),将A,B同时分别向上平移2个单位,再向右平移1个单位,得到的对应点分别为D,C,连接AD,BC.
如图,在直角坐标系xOy中,A(-1,0),B(3,0),将A,B同时分别向上平移2个单位,再向右平移1个单位,得到的对应点分别为D,C,连接AD,BC. 如图,△ABC≌△BAD,若AB=6、AC=4、BC=5,则AD的长为
如图,△ABC≌△BAD,若AB=6、AC=4、BC=5,则AD的长为 如图,已知点O是四边形ABCD内一点,且有OA=OB=OC,∠ABC=70°,则∠AOC=
如图,已知点O是四边形ABCD内一点,且有OA=OB=OC,∠ABC=70°,则∠AOC= 如图,正方形ABCD中,对角线AC与BD相交于点O,DE平分∠CDB交BC于E,交AC于F,则BC:OF=
如图,正方形ABCD中,对角线AC与BD相交于点O,DE平分∠CDB交BC于E,交AC于F,则BC:OF=