题目内容
一个正n边形的每个内角都是它的外角的9倍，则n= ．
考点：多边形内角与外角
专题：
分析：一个多边形的每个内角都是它的外角的9倍，则内角和是外角和的9倍，根据多边形的外角和是360度，即可求得多边形的内角和的度数，依据多边形的内角和公式即可求解．
解答：解：多边形的内角和是：360×9=3240度．
设多边形的边数是n，则
（n-2）•180=3240，
解得：n=20．
即这个多边形是二十边形．
故答案为：20．
设多边形的边数是n，则
（n-2）•180=3240，
解得：n=20．
即这个多边形是二十边形．
故答案为：20．
点评：本题主要考查了多边形的内角和定理以及多边形的外角和定理，注意多边形的外角和不随边数的变化而变化．
练习册系列答案
相关题目
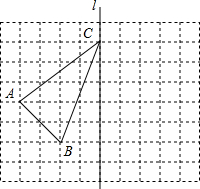如图，在方格纸中，每个小正方形的边长为1，有一个格点△ABC（即三角形的顶点都在格点上），点C在直线l上．
在△ABC中，∠A=60°，∠ABC、∠ACB所对的b、c满足：b2+c2-2（b+c）+2=0．