题目内容
11.一个口袋中放有290个涂有红、黑、白三种颜色的质地相同的小球.若红球个数是黑球个数的2倍多40个.从袋中任取一个球是白球的概率是$\frac{1}{29}$.(1)求袋中红球的个数;
(2)求从袋中任取一个球是黑球的概率.
分析 (1)先根据概率公式求出白球的个数为10,进一步求得红、黑两种球的个数和为280,再根据红球个数是黑球个数的2倍多40个,可得黑球个数为(280-40)÷(2+1)=80个,进一步得到红球的个数;
(2)根据概率公式可求从袋中任取一个球是黑球的概率.
解答 解:(1)290×$\frac{1}{29}$=10(个),
290-10=280(个),
(280-40)÷(2+1)=80(个),
280-80=200(个).
故袋中红球的个数是200个;
(2)80÷290=$\frac{8}{29}$.
答:从袋中任取一个球是黑球的概率是$\frac{8}{29}$.
点评 本题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
1.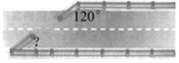 如图所示,要在一条公路的两侧铺设平行管道,已知一侧铺设的角度为120°,为使管道对接,另一侧铺设的角度大小应为( )
如图所示,要在一条公路的两侧铺设平行管道,已知一侧铺设的角度为120°,为使管道对接,另一侧铺设的角度大小应为( )
 如图所示,要在一条公路的两侧铺设平行管道,已知一侧铺设的角度为120°,为使管道对接,另一侧铺设的角度大小应为( )
如图所示,要在一条公路的两侧铺设平行管道,已知一侧铺设的角度为120°,为使管道对接,另一侧铺设的角度大小应为( )| A. | 120° | B. | 100° | C. | 80° | D. | 60° |
2. 如图示,数轴上点A所表示的数的绝对值为( )
如图示,数轴上点A所表示的数的绝对值为( )
 如图示,数轴上点A所表示的数的绝对值为( )
如图示,数轴上点A所表示的数的绝对值为( )| A. | 2 | B. | -2 | C. | ±2 | D. | 以上均不对 |
19.下列说法错误的是( )
| A. | 给定一组数据,那么这组数据的平均数一定只有一个 | |
| B. | 给定一组数据,那么这组数据的中位数一定只有一个 | |
| C. | 给定一组数据,那么这组数据的众数一定只有一个 | |
| D. | 如果一组数据存在众数,那么该众数一定是这组数据中的某一个 |
10.已知x为正整数,y、z与x的关系如表格所示,根据表格中的数字变化规律,解答下列问题.
(1)分别写出y与x,z与x之间的关系式;
(2)是否存在x的值,使得y与z相等?若存在,求出这个值;若不存在,请说明理由.
| x | y | z |
| … | … | … |
| 3 | 10×3+60 | 2×10 |
| 4 | 10×4+60 | 2×11 |
| 5 | 10×5+60 | 2×12 |
| … | … | … |
(2)是否存在x的值,使得y与z相等?若存在,求出这个值;若不存在,请说明理由.
8.关于反比例函数y=$\frac{3}{x}$,下列说法中正确的是( )
| A. | 它的图象分布在第二、四象限 | B. | 它的图象过点(-6,-2) | ||
| C. | 当x<0时,y的值随x的增大而减小 | D. | 与y轴的交点是(0,3) |
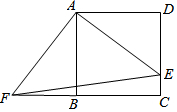 如图,四边形ABCD是正方形,E、F分别是边DC和CB延长线上的点,且DE=BF,连接AE,AF,EF
如图,四边形ABCD是正方形,E、F分别是边DC和CB延长线上的点,且DE=BF,连接AE,AF,EF