题目内容
若x2+x-1=0,求x3+2x2+2的值.
考点:因式分解的应用
专题:
分析:由x2+x-1=0,得出x2+x=1,整体代入代数式x3+2x2+2求得数值即可
解答:
解:∵x2+x-1=0,
∴x2+x=1,
∴x3+2x2+2
=x(x2+x)+x2+2
=x+x2+2
=1+2
=3.
∴x2+x=1,
∴x3+2x2+2
=x(x2+x)+x2+2
=x+x2+2
=1+2
=3.
点评:此题考查提取公因式分解因式法在整式运算中的运用,注意整体思想的渗透.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
已知△ABC,D,E,F分别是AB,BC,CA的中点,设
=
,
=
,则
+
是( )
| AB |
| a |
| AC |
| b |
| DE |
| DF |
A、
| ||||||
B、-
| ||||||
C、
| ||||||
D、
|
 下列各几何体均由三个大小相同的正方体组成,其中正视图为右图的是( )
下列各几何体均由三个大小相同的正方体组成,其中正视图为右图的是( )A、 |
B、 |
C、 |
D、 |
下列计算正确的是( )
| A、a3•a=a3 |
| B、(2a+b)2=4a2+b2 |
| C、a8b÷a2=a4b |
| D、(-3ab3)2=9a2b6 |
 如图,直线AB、CD相交于点O,OE⊥AB于点O,OF平分∠AOE,∠BOD=15°30′,则下列结论中不正确的是( )
如图,直线AB、CD相交于点O,OE⊥AB于点O,OF平分∠AOE,∠BOD=15°30′,则下列结论中不正确的是( )| A、∠AOF=45° |
| B、∠BOD=∠AOC |
| C、∠BOD的余角等于75°30′ |
| D、∠AOD与∠BOD互为补角 |
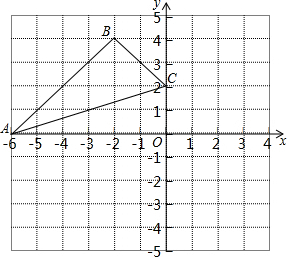 如图,在直角坐标系中,△ABC三个顶点的坐标分别为A(-6,0),B(-2,4),C(0,2).分别以点C,O为位似中心,画出△ABC的位似图形△CDE和△FGH,且同时满足下列两个条件:
如图,在直角坐标系中,△ABC三个顶点的坐标分别为A(-6,0),B(-2,4),C(0,2).分别以点C,O为位似中心,画出△ABC的位似图形△CDE和△FGH,且同时满足下列两个条件: 如图,已知在⊙O中,直径AB与弦CD相交于点P,∠CAB=40°,∠APD=65°.则∠B的度数是
如图,已知在⊙O中,直径AB与弦CD相交于点P,∠CAB=40°,∠APD=65°.则∠B的度数是 如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上).请你根据他们的测量数据计算这棵树的高度.
如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上).请你根据他们的测量数据计算这棵树的高度.