题目内容
9. 如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,BE与CD相交于点F,则下列结论一定正确的是( )
如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,BE与CD相交于点F,则下列结论一定正确的是( )| A. | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | B. | $\frac{DF}{FC}=\frac{AE}{EC}$ | C. | $\frac{AD}{DB}=\frac{DE}{BC}$ | D. | $\frac{DF}{BF}=\frac{EF}{FC}$ |
分析 根据平行线分线段成比例定理与相似三角形的对应边成比例,即可求得答案.
解答 解;A、∵DE∥BC,
∴$\frac{AD}{AB}=\frac{AE}{AC}$,故正确;
B、∵DE∥BC,
∴△DEF∽△CBF,
∴$\frac{DF}{FC}=\frac{EF}{FB}$,故错误;
C、∵DE∥BC,
∴$\frac{AD}{AB}=\frac{DE}{BC}$,故错误;
D、∵DE∥BC,
∴△DEF∽△CBF,
∴$\frac{DF}{FC}=\frac{EF}{BF}$,故错误;
故选:A.
点评 此题考查了相似三角形的判定与性质以及平行线分线段成比例定理.注意掌握各线段的对应关系是解此题的关键.

练习册系列答案
相关题目
19.下列运算正确的是( )
| A. | (-$\frac{3}{2}$)2=-$\frac{9}{4}$ | B. | (3a2)3=9a6 | C. | 5-3÷5-5=$\frac{1}{25}$ | D. | $\sqrt{8}-\sqrt{50}=-3\sqrt{2}$ |
17.关于直线l:y=kx+k(k≠0),下列说法不正确的是( )
| A. | 点(0,k)在l上 | B. | l经过定点(-1,0) | ||
| C. | 当k>0时,y随x的增大而增大 | D. | l经过第一、二、三象限 |
14.省政府提出2016年要实现180 000农村贫困人口脱贫,数据180 000用科学记数法表示为( )
| A. | 1.8×103 | B. | 1.8×104 | C. | 1.8×105 | D. | 1.8×106 |
18.在平面直角坐标系中,若点A(a,-b)在第一象限内,则点B(a,b)所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
19.为加快“最美毕节”环境建设,某园林公司增加了人力进行大型树木移植,现在平均每天比原计划多植树30棵,现在植树400棵所需时间与原计划植树300棵所需时间相同,设现在平均每天植树x棵,则列出的方程为( )
| A. | $\frac{400}{x}=\frac{300}{x-30}$ | B. | $\frac{400}{x-30}=\frac{300}{x}$ | C. | $\frac{400}{x+30}=\frac{300}{x}$ | D. | $\frac{400}{x}=\frac{300}{x+30}$ |

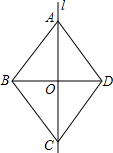 如图,四边形ABCD是轴对称图形,且直线AC是对称轴,AB∥CD,则下列结论:①AC⊥BD;②AD∥BC;③四边形ABCD是菱形;④△ABD≌△CDB.其中正确的是①②③④(只填写序号)
如图,四边形ABCD是轴对称图形,且直线AC是对称轴,AB∥CD,则下列结论:①AC⊥BD;②AD∥BC;③四边形ABCD是菱形;④△ABD≌△CDB.其中正确的是①②③④(只填写序号)