题目内容
 如图,△ABC是⊙O的一个内接三角形,点C是劣弧AB上一点(点C不与A,B重合),设∠OAB=α,∠C=β.
如图,△ABC是⊙O的一个内接三角形,点C是劣弧AB上一点(点C不与A,B重合),设∠OAB=α,∠C=β.(1)当α=35°时,求β的度数;
(2)猜想α与β之间的关系,并给予证明.
考点:圆周角定理
专题:
分析:(1)在优弧AB上取一点D,连结DA、DB,根据三角形内角和定理得∠AOB=180°-∠OAB-∠OBA=110°,再根据圆周角定理得∠D=
∠AOB=55°,然后根据圆内接四边形的性质得∠ACB=180°-∠D=125°,
(2)根据三角形内角和定理得∠AOB=180°-∠α,根据圆周角定理得∠D=
∠AOB=90°-α,然后根据圆内接四边形的性质得∠ACB=180°-∠D=180°-(90°-α)=90°+α.
| 1 |
| 2 |
(2)根据三角形内角和定理得∠AOB=180°-∠α,根据圆周角定理得∠D=
| 1 |
| 2 |
解答: 解:(1)在优弧AB上取一点D,连结DA、DB,如图,
解:(1)在优弧AB上取一点D,连结DA、DB,如图,
∵∠α=35°,
∴∠AOB=180°-∠OAB-∠OBA=180°-2×35°=110°,
∴∠D=
∠AOB=55°,
∴∠ACB=180°-∠D=125°,
即β的度数为125°;
(2)∠ACB=90°+α.理由如下:
∵∠AOB=180°-2∠α,
∴∠D=
∠AOB=
(180°-2∠α)=90°-α,
∴∠ACB=180°-∠D=180°-(90°-α)=90°+α.
 解:(1)在优弧AB上取一点D,连结DA、DB,如图,
解:(1)在优弧AB上取一点D,连结DA、DB,如图,∵∠α=35°,
∴∠AOB=180°-∠OAB-∠OBA=180°-2×35°=110°,
∴∠D=
| 1 |
| 2 |
∴∠ACB=180°-∠D=125°,
即β的度数为125°;
(2)∠ACB=90°+α.理由如下:
∵∠AOB=180°-2∠α,
∴∠D=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠ACB=180°-∠D=180°-(90°-α)=90°+α.
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了圆内接四边形的性质.

练习册系列答案
相关题目

 如图,已知等腰梯形ABCD的底角∠B=45°,高AE=1,上底AD=1,则其面积为
如图,已知等腰梯形ABCD的底角∠B=45°,高AE=1,上底AD=1,则其面积为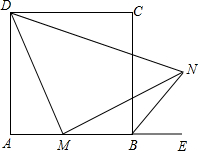 正方形ABCD中,M是AB上的一点,E是AB的延长线上一点,N是∠CBE的平分线上一点,且MN=DM.
正方形ABCD中,M是AB上的一点,E是AB的延长线上一点,N是∠CBE的平分线上一点,且MN=DM. 如图,AC⊥AB于A,BD⊥AB于B,AC=10,BD=6,O为CD的中点,过O作OM⊥AB于M,求OM的长.
如图,AC⊥AB于A,BD⊥AB于B,AC=10,BD=6,O为CD的中点,过O作OM⊥AB于M,求OM的长.