题目内容
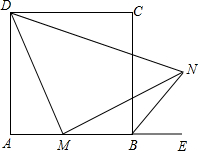 正方形ABCD中,M是AB上的一点,E是AB的延长线上一点,N是∠CBE的平分线上一点,且MN=DM.
正方形ABCD中,M是AB上的一点,E是AB的延长线上一点,N是∠CBE的平分线上一点,且MN=DM.(1)求证:MN⊥DM;
(2)已知AB=2,设AM=x,求DN的长.(用含x的代数式表示)
考点:正方形的性质,全等三角形的判定与性质
专题:
分析:(1)在AD上取一点P,使DP=BM,连接PM,利用正方形的性质,证得△MPD≌△NBM,得出结论;
(2)先在Rt△ADM中利用勾股定理求出DM,再根据△DMN是等腰直角三角形即可求出斜边DN的长.
(2)先在Rt△ADM中利用勾股定理求出DM,再根据△DMN是等腰直角三角形即可求出斜边DN的长.
解答: (1)证明:如图,在AD上取一点P,使DP=BM,连接PM.
(1)证明:如图,在AD上取一点P,使DP=BM,连接PM.
∵四边形ABCD是正方形,
∴AD=AB,∠A=∠ABC=90°.
∵DP=BM,
∴AP=AM,
∴∠APM=45°,∠MPD=135°.
∵BN平分∠CBE,
∴∠CBN=45°,∠NBM=135°.
在钝角△MPD与钝角△NBM中
,
∴△MPD≌△NBM(SSA),
∴∠PDM=∠BMN,
∵∠PDM+∠AMD=90°,
∴∠BMN+∠AMD=90°,
∴∠DMN=90°,
即MN⊥DM;
(2)解:在Rt△ADM中,∵AD=2,设AM=x,∠A=90°,
∴DM=
=
.
∵MN=DM,MN⊥DM,
∴△DMN是等腰直角三角形,
∴DN=
DM=
.
 (1)证明:如图,在AD上取一点P,使DP=BM,连接PM.
(1)证明:如图,在AD上取一点P,使DP=BM,连接PM.∵四边形ABCD是正方形,
∴AD=AB,∠A=∠ABC=90°.
∵DP=BM,
∴AP=AM,
∴∠APM=45°,∠MPD=135°.
∵BN平分∠CBE,
∴∠CBN=45°,∠NBM=135°.
在钝角△MPD与钝角△NBM中
|
∴△MPD≌△NBM(SSA),
∴∠PDM=∠BMN,
∵∠PDM+∠AMD=90°,
∴∠BMN+∠AMD=90°,
∴∠DMN=90°,
即MN⊥DM;
(2)解:在Rt△ADM中,∵AD=2,设AM=x,∠A=90°,
∴DM=
| AM2+AD2 |
| x2+4 |
∵MN=DM,MN⊥DM,
∴△DMN是等腰直角三角形,
∴DN=
| 2 |
| 2x2+8 |
点评:此题考查正方形的性质,三角形全等的判定与性质,勾股定理;把正方形和全等三角形的知识结合起来,巧妙作出辅助线解决问题.注意,SSA一般不能证明两个三角形全等,但是当两个三角形的形状相同时,利用SSA可以判定两个三角形全等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知,在平面直角坐标系xOy中,点A在x轴负半轴上,点B在y轴正半轴上,OA=OB,函数y=-
已知,在平面直角坐标系xOy中,点A在x轴负半轴上,点B在y轴正半轴上,OA=OB,函数y=- 如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点,抛物线的解析式为y=x2-2x-3,AB为半圆的直径,则这个“果圆”被y轴截得的弦CD的长为
如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点,抛物线的解析式为y=x2-2x-3,AB为半圆的直径,则这个“果圆”被y轴截得的弦CD的长为 如图,已知菱形ABCD的边长为2,∠B=60°,点P、Q分别是边BC、CD上的动点(不与端点重合),且BP=CQ.
如图,已知菱形ABCD的边长为2,∠B=60°,点P、Q分别是边BC、CD上的动点(不与端点重合),且BP=CQ. 如图,△ABC是⊙O的一个内接三角形,点C是劣弧AB上一点(点C不与A,B重合),设∠OAB=α,∠C=β.
如图,△ABC是⊙O的一个内接三角形,点C是劣弧AB上一点(点C不与A,B重合),设∠OAB=α,∠C=β.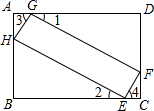 矩形ABCD中,点E,F,G,H分别在BC,CD,DA,AB上,若∠1=∠2=∠3=∠4.
矩形ABCD中,点E,F,G,H分别在BC,CD,DA,AB上,若∠1=∠2=∠3=∠4.