题目内容
1. 如图,在△ABC中,AD平分∠BAC,AB=AC-BD,则∠B:∠C的值为多少?
如图,在△ABC中,AD平分∠BAC,AB=AC-BD,则∠B:∠C的值为多少?
分析 延长AB到E,使得BE=BD,连接DE,由AB+EB=AB+BD,得到AE=AC,利用SAS得到三角形AED与三角形ACD全等,利用全等三角形对应角相等得到一对角相等,再由BE=BD,利用等边对等角得到一对角相等,等量代换即可求出∠B:∠C的值.
解答 解:延长AB到E,使得BE=BD,连接DE,
则AE=AB+BE=AB+BD=AC,
在△EAD和△CAD中,
$\left\{\begin{array}{l}{AE=AC}\\{∠EAD=∠CAD}\\{AD=AD}\end{array}\right.$,
∴△EAD≌△CAD(SAS),
∴∠AED=∠ACD,
∵BE=BD,
∴∠BED=∠BDE,
∵∠ABD=∠BED+∠BDE=2∠BED=2∠ACD,
则∠B=2∠C,
即∠B:∠C=2:1.
点评 此题考查了全等三角形的判定与性质,等腰三角形的性质,以及外角性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
13.在直角坐标系中,O为坐标原点,已知A(2,1),在x轴上确定点P,使△AOP为等腰三角形,则符合条件的点P的个数共有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
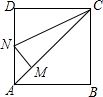 如图,正方形ABCD,CM=CD,MN⊥AC交AD于N,则∠DCN=22.5°,∠MND=135°.
如图,正方形ABCD,CM=CD,MN⊥AC交AD于N,则∠DCN=22.5°,∠MND=135°. 如图,∠1=130°,∠2=130°,∠3=120°,试确定∠4的度数.
如图,∠1=130°,∠2=130°,∠3=120°,试确定∠4的度数.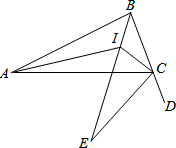 如图,△ABC中,AI、BI分别平分∠BAC、∠ABC,CE是△ABC的外角∠ACD的平分线,交BI延长线于E,连结CI,若AB=1,且△ABC与△ICE相似,那么AC=$\frac{1}{2}$或1或2.
如图,△ABC中,AI、BI分别平分∠BAC、∠ABC,CE是△ABC的外角∠ACD的平分线,交BI延长线于E,连结CI,若AB=1,且△ABC与△ICE相似,那么AC=$\frac{1}{2}$或1或2.