Question

11．已知在△ABC中，AB=2AC，CD⊥AC，AD平分∠BAC，求证：AD=BD．

Answer 1

分析 过D作DE⊥AB于E，根据角平分线的性质得出DE=DC，根据AAS证△DEA≌△DCA，推出AE=AC，利用等腰三角形的性质证明即可．

解答 证明：过D作DE⊥AB于E，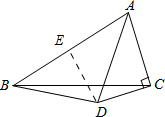

∵AD平分∠BAC，CD⊥AC，
∴DE=DC，
在△DEA和△DCA中，
$\left\{\begin{array}{l}{∠DAE=∠DAC}\\{∠AED=∠ACD}\\{DE=DC}\end{array}\right.$，
∴△DEA≌△DCA，
∴AE=AC，
∵2AC=AB
∴AE=AC=BE
∵AE⊥DE
∴AD=BD

点评 此题考查了等腰三角形的性质，全等三角形的性质和判定的应用，关键是求出△DEA≌△DCA，主要培养了学生分析问题和解决问题的能力，题目比较好，难度适中．