题目内容
3.已知m=$\sqrt{3}$+1,n=$\frac{2}{\sqrt{3}-1}$,则m和n的大小关系为( )| A. | m=n | B. | mn=1 | C. | m=-n | D. | mn=-1 |
分析 首先根据分母有理化的方法,把n=$\frac{2}{\sqrt{3}-1}$分母有理化,然后再把它和m比较大小,判断出m和n的大小关系;最后求出mn的值是多少即可.
解答 解:因为n=$\frac{2}{\sqrt{3}-1}$=$\frac{2(\sqrt{3}+1)}{(\sqrt{3}-1)(\sqrt{3}+1)}=\sqrt{3}+1$,m=$\sqrt{3}$+1,
所以m=n;
又因为mn=$(\sqrt{3}+1)×(\sqrt{3}+1)$
=4$+2\sqrt{3}$
所以mn≠1,mn≠-1,
所以选项B、D错误.
故选:A.
点评 (1)此题主要考查了分母有理化的含义,以及分母有理化的方法,要熟练掌握,解答此题的关键是把n=$\frac{2}{\sqrt{3}-1}$分母有理化.
(2)此题还考查了整式乘法的运算方法,要熟练掌握.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
13. 阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.1995年联合国教科文组织把每年4月23日确定为“世界读书日”.如图是某校三个年级学生人数分布扇形统计图,其中九年级人数为408人,下表是该校学生阅读课外书籍情况统计表.请你根据图表中的信息,解答下列问题:
阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.1995年联合国教科文组织把每年4月23日确定为“世界读书日”.如图是某校三个年级学生人数分布扇形统计图,其中九年级人数为408人,下表是该校学生阅读课外书籍情况统计表.请你根据图表中的信息,解答下列问题:
(1)求该校九年级的人数占全校总人数的百分率是34%.
(2)求表中A,B的值;A=600,B=0.35.
(3)该校学生平均每人读多少本课外书?
(4)某新华书店新进一种科普常识类课外书籍,其进价是每本6元,这种课外书的月销售量y(本)是每本的销售价x(元)的一次函数,且当x=8时y=120;当x=10时y=100.为答谢广大读者,让利顾客,请计算该新华书店的这种课外书月销售利润为330元时的销售单价.
 阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.1995年联合国教科文组织把每年4月23日确定为“世界读书日”.如图是某校三个年级学生人数分布扇形统计图,其中九年级人数为408人,下表是该校学生阅读课外书籍情况统计表.请你根据图表中的信息,解答下列问题:
阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.1995年联合国教科文组织把每年4月23日确定为“世界读书日”.如图是某校三个年级学生人数分布扇形统计图,其中九年级人数为408人,下表是该校学生阅读课外书籍情况统计表.请你根据图表中的信息,解答下列问题:| 图书种类 | 频数 | 频率 |
| 科普常识 | 840 | B |
| 名人传记 | 816 | 0.34 |
| 漫画丛书 | A | 0.25 |
| 其他 | 144 | 0.06 |
(2)求表中A,B的值;A=600,B=0.35.
(3)该校学生平均每人读多少本课外书?
(4)某新华书店新进一种科普常识类课外书籍,其进价是每本6元,这种课外书的月销售量y(本)是每本的销售价x(元)的一次函数,且当x=8时y=120;当x=10时y=100.为答谢广大读者,让利顾客,请计算该新华书店的这种课外书月销售利润为330元时的销售单价.
14.下列实数中,为无理数的是( )
| A. | $\sqrt{4}$ | B. | $\root{3}{64}$ | C. | $\sqrt{11}$ | D. | -3.5 |
13. 如图,△ABC中,E为边BC延长线上一点,∠ABC的平分线与∠ACE的平分线交于点D,若∠A=46°,则∠D的度数为( )
如图,△ABC中,E为边BC延长线上一点,∠ABC的平分线与∠ACE的平分线交于点D,若∠A=46°,则∠D的度数为( )
 如图,△ABC中,E为边BC延长线上一点,∠ABC的平分线与∠ACE的平分线交于点D,若∠A=46°,则∠D的度数为( )
如图,△ABC中,E为边BC延长线上一点,∠ABC的平分线与∠ACE的平分线交于点D,若∠A=46°,则∠D的度数为( )| A. | 46° | B. | 92° | C. | 44° | D. | 23° |
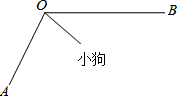 如图,OA、OB是某墙角处的两条地脚线,夹角∠AOB=150°,一根4米长的绳子一端拴在墙角O处(OA>4米,OB>4米),另一端栓一只小狗,小狗在地面上活动,求
如图,OA、OB是某墙角处的两条地脚线,夹角∠AOB=150°,一根4米长的绳子一端拴在墙角O处(OA>4米,OB>4米),另一端栓一只小狗,小狗在地面上活动,求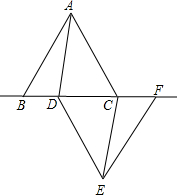 如图,已知△ABC和△DEF是两个边长都为10cm的等边三角形,且B、D、C、F都在同一条直线上,连接AD、CE.
如图,已知△ABC和△DEF是两个边长都为10cm的等边三角形,且B、D、C、F都在同一条直线上,连接AD、CE.