题目内容
11.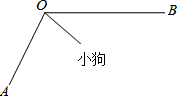 如图,OA、OB是某墙角处的两条地脚线,夹角∠AOB=150°,一根4米长的绳子一端拴在墙角O处(OA>4米,OB>4米),另一端栓一只小狗,小狗在地面上活动,求
如图,OA、OB是某墙角处的两条地脚线,夹角∠AOB=150°,一根4米长的绳子一端拴在墙角O处(OA>4米,OB>4米),另一端栓一只小狗,小狗在地面上活动,求(1)小狗可活动的最大区域图形的周长;
(2)小狗可活动的最大区域图形的面积(结果保留π).
分析 由题意得,小狗可活动的区域为一个扇形,此扇形为OAB,圆心角为150°,半径为4m.
(1)根据弧长公式进行计算;
(2)根据扇形面积进行计算.
解答 解:(1)小狗可活动的最大区域图形的周长为:$\frac{150π×4}{180}$=$\frac{10π}{3}$(米);
(2)小狗可活动的最大区域图形的面积为:$\frac{150×{4}^{2}π}{360}$=$\frac{20π}{3}$(米2).
答:(1)小狗可活动的最大区域图形的周长是$\frac{10π}{3}$米;
(2)小狗可活动的最大区域图形的面积是$\frac{20π}{3}$米2.
点评 本题考查了扇形面积和弧长的计算在实际问题中的运用.熟记公式是解题的关键.

练习册系列答案
相关题目
2.抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如表所示.抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如表
从上表可知,下列说法正确的个数为( )
①抛物线与x轴的一个交点为(-2,0);
②抛物线与y轴的交点为(0,6);
③抛物线的对称轴是x=$\frac{1}{2}$;
④抛物线与x轴的另一个交点为(3,0);
⑤在对称轴左侧,y随x增大而减小.
| x | … | -3 | -2 | -1 | 0 | 1 | … |
| y | … | -6 | 0 | 4 | 6 | 6 | … |
①抛物线与x轴的一个交点为(-2,0);
②抛物线与y轴的交点为(0,6);
③抛物线的对称轴是x=$\frac{1}{2}$;
④抛物线与x轴的另一个交点为(3,0);
⑤在对称轴左侧,y随x增大而减小.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
6.方程组$\left\{\begin{array}{l}{3x-5y=6,①}\\{2x-3y=4,②}\end{array}\right.$将②×3-①×2得( )
| A. | -3y=2 | B. | 4y+1=0 | C. | y=0 | D. | x-2y=2 |
3.已知m=$\sqrt{3}$+1,n=$\frac{2}{\sqrt{3}-1}$,则m和n的大小关系为( )
| A. | m=n | B. | mn=1 | C. | m=-n | D. | mn=-1 |
20.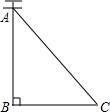 如图,AC是电线杆AB的一根拉线,测得BC的长为6米,∠ACB=50°,则拉线AC的长为( )
如图,AC是电线杆AB的一根拉线,测得BC的长为6米,∠ACB=50°,则拉线AC的长为( )
 如图,AC是电线杆AB的一根拉线,测得BC的长为6米,∠ACB=50°,则拉线AC的长为( )
如图,AC是电线杆AB的一根拉线,测得BC的长为6米,∠ACB=50°,则拉线AC的长为( )| A. | $\frac{6}{sin50°}$米 | B. | $\frac{6}{tan50°}$米 | C. | 6cos50°米 | D. | $\frac{6}{cos50°}$米 |
1.若平行四边形中两个内角的度数比为1:2,则其中较小的内角是( )
| A. | 60° | B. | 90° | C. | 120° | D. | 45° |
 在RtABC中,∠C=90°,AC=BC=$\sqrt{2}$(如图),若将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,联结C′B,则C′B的长为$\sqrt{3}$-1.
在RtABC中,∠C=90°,AC=BC=$\sqrt{2}$(如图),若将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,联结C′B,则C′B的长为$\sqrt{3}$-1. 如图所示,三角形OAB的顶点B的坐标为(4,0),把三角形OAB沿x轴向右平移得到三角形CDE,如果CB=1,那么OE的长为7.
如图所示,三角形OAB的顶点B的坐标为(4,0),把三角形OAB沿x轴向右平移得到三角形CDE,如果CB=1,那么OE的长为7.