题目内容
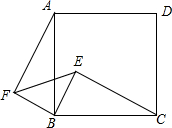 已知四边形ABCD是正方形,E是正方形内一点,以BC为斜边作直角三角形BCE,又以BE为直角边作等腰直角三角形EBF,且∠EBF=90°,连结AF.
已知四边形ABCD是正方形,E是正方形内一点,以BC为斜边作直角三角形BCE,又以BE为直角边作等腰直角三角形EBF,且∠EBF=90°,连结AF.(1)AF与CE相等吗?试说明理由.
(2)AF与EB存在怎样的位置关系?试说明理由.
考点:全等三角形的判定与性质,正方形的性质
专题:常规题型
分析:(1)易证△ABF≌△CBE,可得AF=CE;
(2)垂直.根据平行线的传递性可解本题.
(2)垂直.根据平行线的传递性可解本题.
解答:解:(1)∵∠ABF+∠ABE=90°,∠CBE+∠ABE=90°
∵在△ABF和△CBE中,
,
∴△ABF≌△CBE(SAS),
∴AF=CE;
(2)∵△ABF≌△CBE
∴∠AFB=∠CEB=90°,
∵等腰直角三角形EBF中,∠BEF=∠BFE=45°
∴∠AFE=90°-45°=45°=∠BEF,
∴AF∥DE,
∵BE⊥CE
∴AF⊥CE.
∵在△ABF和△CBE中,
|
∴△ABF≌△CBE(SAS),
∴AF=CE;
(2)∵△ABF≌△CBE
∴∠AFB=∠CEB=90°,
∵等腰直角三角形EBF中,∠BEF=∠BFE=45°
∴∠AFE=90°-45°=45°=∠BEF,
∴AF∥DE,
∵BE⊥CE
∴AF⊥CE.
点评:本题考查了全等三角形的判定,考查了全等三角形对应角、对应边相等的性质,考查了平行线的传递性,本题中求证△ABF≌△CBE是解题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
下列长度的三条线段中,能组成三角形的是( )
| A、3cm,5cm,8cm |
| B、8cm,8cm,18cm |
| C、1cm,1cm,1cm |
| D、3cm,12cm,8cm |
 如图,在☉O中直径为AB=10,弦CD⊥AB,垂足为点E,OE=3,弦CD的长是
如图,在☉O中直径为AB=10,弦CD⊥AB,垂足为点E,OE=3,弦CD的长是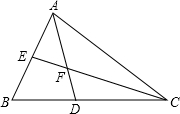 如图,在△ABC中,∠B=60°,∠BAC、∠ACB的平分线AD、CE交于点F,试猜想AE、CD、AC三条线段之间的数量关系,并加以证明.
如图,在△ABC中,∠B=60°,∠BAC、∠ACB的平分线AD、CE交于点F,试猜想AE、CD、AC三条线段之间的数量关系,并加以证明. 如图,△ABC中,AB=AC,∠A=100°,CD平分∠ACB交AB于D,E为BC上一点,BE=DE.求证:BC=CD+AD.
如图,△ABC中,AB=AC,∠A=100°,CD平分∠ACB交AB于D,E为BC上一点,BE=DE.求证:BC=CD+AD.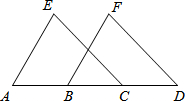 已知:如图,AB=DC,AE=BF,CE=DF,∠A=60°.
已知:如图,AB=DC,AE=BF,CE=DF,∠A=60°.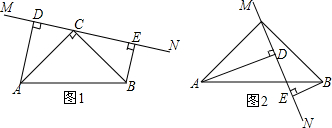
 已知:如图,AB=DC,AD=BC,O是DB的中点,过O点的直线分别交DA和BC的延长线于E,F.求证:∠E=∠F.
已知:如图,AB=DC,AD=BC,O是DB的中点,过O点的直线分别交DA和BC的延长线于E,F.求证:∠E=∠F.