题目内容
如图，在☉O中直径为AB=10，弦CD⊥AB，垂足为点E，OE=3，弦CD的长是考点：垂径定理,勾股定理
专题：
分析：连接OC，先根据直径AB=10求出OC的长，再根据勾股定理求出CE的长，由垂径定理即可得出结论．
解答：
解：连接OC，
∵直径AB=10，
∴OC=
AB=5，
∵CD⊥AB，OE=3，
∴CD=2CE，
在Rt△OCE中，CE2+OE2=OC2，即CE2+32=52，解得CE=4，
∴CD=2CE=2×4=8．
故答案为：8．
解：连接OC，∵直径AB=10，
∴OC=
| 1 |
| 2 |
∵CD⊥AB，OE=3，
∴CD=2CE，
在Rt△OCE中，CE2+OE2=OC2，即CE2+32=52，解得CE=4，
∴CD=2CE=2×4=8．
故答案为：8．
点评：本题考查的是垂径定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
相关题目
下列说法不正确的是（ ）
| A、-6是36的一个平方根 |
| B、6是36的一个平方根 |
| C、36的平方根是6 |
| D、36的平方根是±6 |
下列各组数中互为相反数的是（ ）
A、5和
| |||
B、-5和
| |||
C、-5和
| |||
| D、-|-5|和-（-5） |
如图，等腰△ABC中，AC=BC，△BDC和△ACE分别为等边三角形，AE与BD相交于点F，连接CF并延长，交AB于点G．求证：G为AB的中点．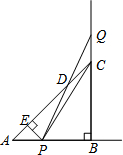
如图，等腰直角三角形ABC中，∠ABC=90°，AB=BC=2，点P、Q分别从A、C两点同时出发，以相同速度作直线运动，点P沿射线AB向右运动，点Q沿BC边的延长线向上运动．设线段PQ与直线AC交于点D，AP的长为x，△PCQ的面积为S．
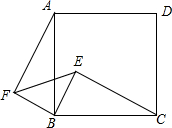已知四边形ABCD是正方形，E是正方形内一点，以BC为斜边作直角三角形BCE，又以BE为直角边作等腰直角三角形EBF，且∠EBF=90°，连结AF．