题目内容
19. 图中的四边形均是矩形,根据图形,写出一个正确的等式:
图中的四边形均是矩形,根据图形,写出一个正确的等式:(a+b)2=a2+2ab+b2.
分析 根据图形,将正方形的面积运用两种不同的方式表达出来,即可得到等式(a+b)2=a2+2ab+b2.
解答 解:由图可得,
正方形的面积=(a+b)2,
正方形的面积=a2+2ab+b2,
则(a+b)2=a2+2ab+b2.
故答案为:(a+b)2=a2+2ab+b2.
点评 本题主要参考了完全平方公式的几何背景,解决问题的关键是:用大正方形的面积等于边长为a和边长为b的两个正方形与两个长宽分别是a,b的长方形的面积的和作为相等关系.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
9.某超市推出如下购物优惠方案:(1)一次性购物在80元(不含80元)以内时,不享受优惠;(2)一次性购物在80元(含80元)以上,300元(不含300元)以内时,一律享受九折的优惠;(3)一次性购物在300元(含300元)以上时,一律享受八折的优惠,某顾客在本超市两次购物分别付款65元、252元,如果他改成在本超市一次性购买与上两次完全相同的商品,则应付款( )
| A. | 316元 | B. | 304元或316元 | C. | 276元 | D. | 276元或304元 |
9.邻补角是( )
| A. | 和为180°的两个角 | |
| B. | 有公共顶点且有一条公共边,另一边互为反向延长线的两个角 | |
| C. | 有一条公共边且相等的两个角 | |
| D. | 有公共顶点且互补的两个角 |
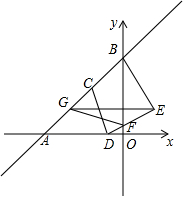 如图,在平面直角坐标系中,直线y=x+2分别交x轴、y轴于点A、B,设C为AB的中点,D是线段OA上的动点(OD<1),连结CD,将CD绕点D顺时针旋转90°至DE,交y轴于点F,过点E作x轴的平行线交AB于点G,连结FG,BE,则四边形BEFG面积的最小值为$\frac{7}{4}$.
如图,在平面直角坐标系中,直线y=x+2分别交x轴、y轴于点A、B,设C为AB的中点,D是线段OA上的动点(OD<1),连结CD,将CD绕点D顺时针旋转90°至DE,交y轴于点F,过点E作x轴的平行线交AB于点G,连结FG,BE,则四边形BEFG面积的最小值为$\frac{7}{4}$.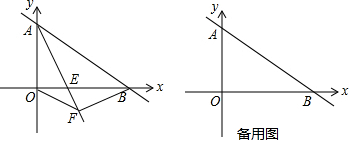
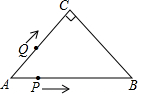 如图,在等腰Rt△ABC中,∠C=90°,AC=4$\sqrt{2}$cm,两个动点P,Q同时从点A出发,点P以1cm/s的速度沿AB运动,点Q以$\sqrt{2}$cm/s的速度沿折线AC-CB运动.当点P到达B时,P,Q停止运动,设运动时间为t秒.则当t=2$\sqrt{2}$或4+2$\sqrt{2}$秒时,△APQ的面积为4cm2.
如图,在等腰Rt△ABC中,∠C=90°,AC=4$\sqrt{2}$cm,两个动点P,Q同时从点A出发,点P以1cm/s的速度沿AB运动,点Q以$\sqrt{2}$cm/s的速度沿折线AC-CB运动.当点P到达B时,P,Q停止运动,设运动时间为t秒.则当t=2$\sqrt{2}$或4+2$\sqrt{2}$秒时,△APQ的面积为4cm2. 如图,在矩形ABCD中,点O在对角线AB上,以OA的长为半径的圆O与AD交于点E,
如图,在矩形ABCD中,点O在对角线AB上,以OA的长为半径的圆O与AD交于点E,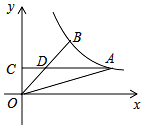 如图,A,B是反比例函数y=$\frac{k}{x}$图象上的两点,过点A作AC⊥y轴,垂足为C,AC交OB于点D.若D为OB的中点,△AOD的面积为6,则k的值为16.
如图,A,B是反比例函数y=$\frac{k}{x}$图象上的两点,过点A作AC⊥y轴,垂足为C,AC交OB于点D.若D为OB的中点,△AOD的面积为6,则k的值为16.