题目内容
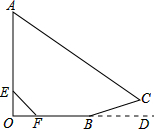 小明利用旗杆在阳光下的影长来测量旗杆的高度.如图,旗杆OA直立在地面OD上,在某一时刻,他的影子由OB、BC两部分组成,测得OB为8m,BC为2m,其中BC在斜坡上,∠CBD=15°.小明在旗杆OA上取了一点E,使得OE为1m,测得OE的影长OF为1m.
小明利用旗杆在阳光下的影长来测量旗杆的高度.如图,旗杆OA直立在地面OD上,在某一时刻,他的影子由OB、BC两部分组成,测得OB为8m,BC为2m,其中BC在斜坡上,∠CBD=15°.小明在旗杆OA上取了一点E,使得OE为1m,测得OE的影长OF为1m.(1)求∠A的度数;
(2)求旗杆OA的高度.
考点:相似三角形的应用,平行投影
专题:计算题
分析:(1)由OE=OF=1,可判断△OEF为直角三角形,则∠OEF=45°,根据平行投影得到EF∥AC,所以∠A=∠OEF=45°;
(2)作CD⊥OB于D,AC的延长线交OB于G,如图,在Rt△BCD中,根据锐角三角函数的定义得CD=2sin15°≈0.52,BD=2cos15°≈1.93,再判断△CDG为等腰直角三角形,则DG=CD=0.52,然后计算OG=OB+BD+DG=10.45,所以OA=OG=10.45.
(2)作CD⊥OB于D,AC的延长线交OB于G,如图,在Rt△BCD中,根据锐角三角函数的定义得CD=2sin15°≈0.52,BD=2cos15°≈1.93,再判断△CDG为等腰直角三角形,则DG=CD=0.52,然后计算OG=OB+BD+DG=10.45,所以OA=OG=10.45.
解答:解:(1)∵OA⊥OB,
∴∠AOB=90°,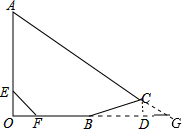
∵OE=OF=1,
∴△OEF为直角三角形,
∴∠OEF=45°,
∵EF∥AC,
∴∠A=∠OEF=45°;
(2)作CD⊥OB于D,AC的延长线交OB于G,如图,
在Rt△BCD中,∵sin∠CBD=sin15°=
,cos∠CBD=cos15°=
,
∴CD=2sin15°≈0.52,BD=2cos15°≈1.93,
∵CD∥AO,
∴△CDG为等腰直角三角形,
∴DG=CD=0.52,
∴OG=OB+BD+DG=8+1.93+0.52=10.45,
∴OA=OG=10.45,
即旗杆OA的高度为10.45m.
∴∠AOB=90°,

∵OE=OF=1,
∴△OEF为直角三角形,
∴∠OEF=45°,
∵EF∥AC,
∴∠A=∠OEF=45°;
(2)作CD⊥OB于D,AC的延长线交OB于G,如图,
在Rt△BCD中,∵sin∠CBD=sin15°=
| CD |
| BC |
| BD |
| BC |
∴CD=2sin15°≈0.52,BD=2cos15°≈1.93,
∵CD∥AO,
∴△CDG为等腰直角三角形,
∴DG=CD=0.52,
∴OG=OB+BD+DG=8+1.93+0.52=10.45,
∴OA=OG=10.45,
即旗杆OA的高度为10.45m.
点评:本题考查了相似三角形的应用:利用影长测量物体的高度;利用相似测量河的宽度(测量距离);借助标杆或直尺测量物体的高度.也考查了平行投影.

练习册系列答案
相关题目
 如图,若DB⊥AE于B,DC⊥AF于C,延长BD交AF于点G,且DC=BD,∠ADG=120°,则下列结论正确的是:
如图,若DB⊥AE于B,DC⊥AF于C,延长BD交AF于点G,且DC=BD,∠ADG=120°,则下列结论正确的是: 如图,已知梯形上下底边的长分别为36和60,高为32,这个梯形两腰的延长线的交点到两底的距离分别是多少?
如图,已知梯形上下底边的长分别为36和60,高为32,这个梯形两腰的延长线的交点到两底的距离分别是多少?