题目内容
如图，已知梯形上下底边的长分别为36和60，高为32，这个梯形两腰的延长线的交点到两底的距离分别是多少？考点：相似三角形的判定与性质,梯形
专题：
分析：设两腰的延长线交于点E，过E作EG⊥CD，交AB于点F，交CD于点G，则FG=32，由条件可得△EAB∽△EDC，可得
=
，且EG=EF+FG，代入可求得EF，进一步可求得EG．
| EF |
| EG |
| AB |
| CD |
解答：
解：如图，设两腰的延长线交于点E，过E作EG⊥CD，交AB于点F，交CD于点G，则EF⊥AB，FG=32，
∵AB∥CD，
∴△EAB∽△EDC，
∴
=
，且EG=EF+FG=EF+32，
∴
=
，
解得EF=
，
则EG=
+32=
，
即梯形两腰的延长线的交点到两底的距离分别为
和
．
解：如图，设两腰的延长线交于点E，过E作EG⊥CD，交AB于点F，交CD于点G，则EF⊥AB，FG=32，∵AB∥CD，
∴△EAB∽△EDC，
∴
| EF |
| EG |
| AB |
| CD |
∴
| EF |
| EF+32 |
| 36 |
| 60 |
解得EF=
| 64 |
| 3 |
则EG=
| 64 |
| 3 |
| 160 |
| 3 |
即梯形两腰的延长线的交点到两底的距离分别为
| 64 |
| 3 |
| 160 |
| 3 |
点评：本题主要考查相似三角形的判定和性质，掌握相似三角形对应高的比等于相似比是解题的关键，注意方程思想的应用．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
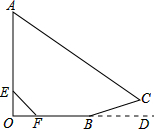小明利用旗杆在阳光下的影长来测量旗杆的高度．如图，旗杆OA直立在地面OD上，在某一时刻，他的影子由OB、BC两部分组成，测得OB为8m，BC为2m，其中BC在斜坡上，∠CBD=15°．小明在旗杆OA上取了一点E，使得OE为1m，测得OE的影长OF为1m．
如图，在△ABC中，DE∥BC，DF∥AC，AE=4，EC=2，BC=8，求BF和CF的长．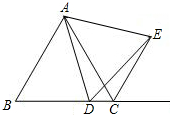
如图，已知△ABC为等边三角形，∠ADE=60°，CE为外角角平分线，求证：△ADE为等边三角形．