题目内容
已知AB是⊙O的直径,AB=10,弦BC=6,点D在⊙O上与点C在AB两侧,过点D作⊙O的切线PD.
(1)如图1,PD与AB延长线交于点P,连接PC,若PC与⊙C相切,求弦AD、CD的长.
(2)如图2,若切线PD∥AB,求弦AD、CD的长.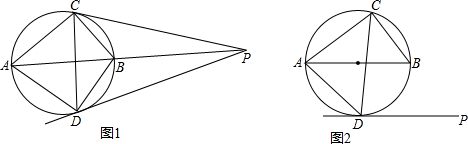
(1)如图1,PD与AB延长线交于点P,连接PC,若PC与⊙C相切,求弦AD、CD的长.
(2)如图2,若切线PD∥AB,求弦AD、CD的长.

考点:切线的性质
专题:计算题
分析:(1)连结OD,如图1,根据切线长定理得到PC=PD,OP平分∠CPD,再利用等腰三角形的性质得到PA⊥CD,则根据垂径定理得到
=
,CE=DE,所以BD=BC=6,然后根据圆周角定理由AB为直径得到∠ADB=90°,于是可根据勾股定理计算出AD=8;接着利用面积法计算出DE,从而得到CD的长;
(2)作DE⊥AC于E,DF⊥BC于F,连结OD、OB,如图2,根据切线的性质由PD为⊙O的切线得PD⊥OD,利用AB∥PD得到OD⊥AB,则根据垂径定理得到
=
,
所以AD=BD,利用AB为直径得到∠ADB=90°,∠ACB=90°,于是可判断△ABD为等腰直角三角形,所以AD=
AB=5
;在Rt△ACB中勾股定理可计算出AC=8,接着由四边形DECF为正方形得到CE=CF,证明Rt△DAE≌Rt△DBF得到AE=BF,然后计算出CE=7,最后根据正方形的性质得到CD=
CE=7
.
 |
| BC |
 |
| BD |
(2)作DE⊥AC于E,DF⊥BC于F,连结OD、OB,如图2,根据切线的性质由PD为⊙O的切线得PD⊥OD,利用AB∥PD得到OD⊥AB,则根据垂径定理得到
 |
| AD |
 |
| BD |
所以AD=BD,利用AB为直径得到∠ADB=90°,∠ACB=90°,于是可判断△ABD为等腰直角三角形,所以AD=
| ||
| 2 |
| 2 |
| 2 |
| 2 |
解答:(1)解: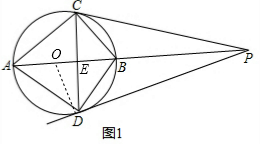 连结OD,如图1,
连结OD,如图1,
∵PC和PD为⊙O的切线,
∴PC=PD,OP平分∠CPD,
∴PA⊥CD,
∴
=
,CE=DE,
∴BD=BC=6,
∵AB为直径,
∴∠ADB=90°,
∴AD=
=
=8;
∵
DE•AB=
AD•BD,
∴DE=
=
,
∴CD=2DE=
;
(2)作DE⊥AC于E,DF⊥BC于F,连结OD、OB,如图2,
∵PD为⊙O的切线,
∴PD⊥OD,
∵AB∥PD,
∴OD⊥AB,
∴
=
,
∴AD=BD,
∵AB为直径,
∴∠ADB=90°,∠ACB=90°,
∴△ABD为等腰直角三角形,
∴AD=
AB=5
,
在Rt△ACB中,∵BC=6,AB=10,
∴AC=
=8,
∵
=
,
∴∠ACD=∠BCD,
∴DE=DF,
∴四边形DECF为正方形,
∴CE=CF,
在Rt△DAE和Rt△DBF中,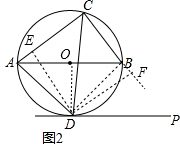
,
∴Rt△DAE≌Rt△DBF,
∴AE=BF,
∴AC+BC=CE+AE+CF-BF=2CE,
∴2CE=6+8=14,解得CE=7,
而四边形DECF为正方形,
∴CD=
CE=7
.
 连结OD,如图1,
连结OD,如图1,∵PC和PD为⊙O的切线,
∴PC=PD,OP平分∠CPD,
∴PA⊥CD,
∴
 |
| BC |
 |
| BD |
∴BD=BC=6,
∵AB为直径,
∴∠ADB=90°,
∴AD=
| AB2-BD2 |
| 102-62 |
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴DE=
| 6×8 |
| 10 |
| 24 |
| 5 |
∴CD=2DE=
| 48 |
| 5 |
(2)作DE⊥AC于E,DF⊥BC于F,连结OD、OB,如图2,
∵PD为⊙O的切线,
∴PD⊥OD,
∵AB∥PD,
∴OD⊥AB,
∴
 |
| AD |
 |
| BD |
∴AD=BD,
∵AB为直径,
∴∠ADB=90°,∠ACB=90°,
∴△ABD为等腰直角三角形,
∴AD=
| ||
| 2 |
| 2 |
在Rt△ACB中,∵BC=6,AB=10,
∴AC=
| AB2-BC2 |
∵
 |
| AD |
 |
| BD |
∴∠ACD=∠BCD,
∴DE=DF,
∴四边形DECF为正方形,
∴CE=CF,
在Rt△DAE和Rt△DBF中,

|
∴Rt△DAE≌Rt△DBF,
∴AE=BF,
∴AC+BC=CE+AE+CF-BF=2CE,
∴2CE=6+8=14,解得CE=7,
而四边形DECF为正方形,
∴CD=
| 2 |
| 2 |
点评:本题考查了切线的性质:①圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了切线长定理和等腰三角形的性质.

练习册系列答案
相关题目
α,β是方程x2+2x-5=0的两个实数根,则α2+2α+αβ的值为( )
| A、5 | B、-5 | C、0 | D、10 |
下列分式中,不可能等于0的是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
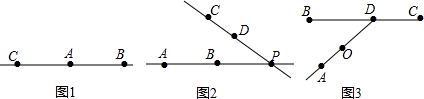
 将图中标有弧线的角表示出来.
将图中标有弧线的角表示出来.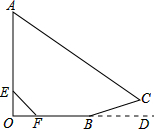 小明利用旗杆在阳光下的影长来测量旗杆的高度.如图,旗杆OA直立在地面OD上,在某一时刻,他的影子由OB、BC两部分组成,测得OB为8m,BC为2m,其中BC在斜坡上,∠CBD=15°.小明在旗杆OA上取了一点E,使得OE为1m,测得OE的影长OF为1m.
小明利用旗杆在阳光下的影长来测量旗杆的高度.如图,旗杆OA直立在地面OD上,在某一时刻,他的影子由OB、BC两部分组成,测得OB为8m,BC为2m,其中BC在斜坡上,∠CBD=15°.小明在旗杆OA上取了一点E,使得OE为1m,测得OE的影长OF为1m.