题目内容
如图，?ABCD中，AB=10，AD=8，AC⊥BC，求AC、OA以及?ABCD的面积．考点：平行四边形的性质
专题：
分析：直接利用平行四边形对边相等得出BC=AD=8，再利用勾股定理得出AC的长，结合平行四边形对角线互相平分以及利用平行四边形面积公式求出即可．
解答：解：∵?ABCD中，AB=10，AD=8，AC⊥BC，
∴BC=8，则AC=
=6，
∴AO=CO=3，
∴?ABCD的面积为：AC×BC=6×8=48．
∴BC=8，则AC=
| AB2-BC2 |
∴AO=CO=3，
∴?ABCD的面积为：AC×BC=6×8=48．
点评：此题主要考查了平行四边形的面积以及其性质和勾股定理等知识，得出BC的长是解题关键．
练习册系列答案
相关题目
如图，AB∥CD，AF与CD交于点E，BE⊥AF，∠B=60°，则∠DEF的度数是（ ）| A、10° | B、20° |
| C、30° | D、40° |
已知下列命题：
①若a＞0，b＞0，则a+b＞0；
②若a=b，则a2=b2；
③角的平分线上的点到角的两边的距离相等；
④矩形的对角线相等．
其中原命题与逆命题均为真命题的个数是（ ）
①若a＞0，b＞0，则a+b＞0；
②若a=b，则a2=b2；
③角的平分线上的点到角的两边的距离相等；
④矩形的对角线相等．
其中原命题与逆命题均为真命题的个数是（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
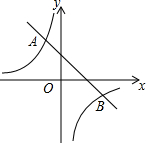如图，一次函数y=-2x+b（b为常数）的图象与反比例函数y=