题目内容
5.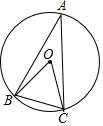 如图,⊙O是△ABC的外接圆,⊙O的半径为2,∠A=30°,则BC=( )
如图,⊙O是△ABC的外接圆,⊙O的半径为2,∠A=30°,则BC=( )| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 2 | D. | $\frac{1}{3}π$ |
分析 先根据圆周角定理求出∠BOC的度数,进而可得出结论.
解答 解:∵∠A=30°,
∴∠BOC=2∠A=60°,
∴△OBC是等边三角形.
∵⊙O的半径为2,
∴BC=2.
故选C.
点评 本题考查的是三角形的外接圆与外心,熟知圆周角定理是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.计算$\sqrt{2}$×$\sqrt{8}$+$\root{3}{-27}$的结果为( )
| A. | ±1 | B. | 1 | C. | 4-3$\sqrt{3}$ | D. | 7 |
16.下列事件中,是确定性事件的是( )
| A. | 甲、乙、丙三人随意站成一排,而甲恰好站中间 | |
| B. | 从含有1个次品的10个产品中,随意抽取一个产品恰好是次品 | |
| C. | 早晨,太阳从西方升起 | |
| D. | 明天早晨八点是上班高峰期,学校门前的公路上必塞 |
10.下列计算中,正确的是( )
| A. | x2+x4=x6 | B. | 2x+3y=5xy | C. | (x3)2=x6 | D. | x6÷x3=x2 |
17.下列计算正确的是( )
| A. | 3a+4b=7ab | B. | (ab3)3=ab6 | C. | x12÷x6=x6 | D. | (a+2)2=a2+4 |
14. 如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=-$\frac{1}{2}$x的图象交于点A(-2,m)和点B,则点B的坐标是( )
如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=-$\frac{1}{2}$x的图象交于点A(-2,m)和点B,则点B的坐标是( )
 如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=-$\frac{1}{2}$x的图象交于点A(-2,m)和点B,则点B的坐标是( )
如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=-$\frac{1}{2}$x的图象交于点A(-2,m)和点B,则点B的坐标是( )| A. | (2,-1) | B. | (1,-2) | C. | ($\frac{1}{2}$,-1) | D. | ( 1,-$\frac{1}{2}$) |
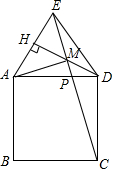 如图,正方形ABCD,点E在正方形外侧且DE=CD,DH⊥AE,垂足为H交CE于M.
如图,正方形ABCD,点E在正方形外侧且DE=CD,DH⊥AE,垂足为H交CE于M.