题目内容
15.在△ABC中,∠C=90°,D在边AC上,且AD=BD=5,CD=3,求tan∠CBD和cosA的值.分析 Rt△BCD中根据勾股定理求得BC的长,由tan∠CBD=$\frac{CD}{BC}$可得;由AC=AD+CD=5+3=8、BC=4根据勾股定理求得AB的长后,由cosA=$\frac{AC}{AB}$可得答案.
解答 解:如图,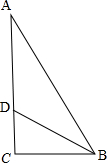
∵在Rt△BCD中,BD=5、CD=3,
∴BC=$\sqrt{B{D}^{2}-C{D}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴tan∠CBD=$\frac{CD}{BC}$=$\frac{3}{4}$;
∵AC=AD+CD=5+3=8,BC=4,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{8}^{2}+{4}^{2}}$=4$\sqrt{5}$,
∴cosA=$\frac{AC}{AB}$=$\frac{8}{4\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$.
点评 本题主要考查解直角三角形,熟练掌握勾股定理和三角函数的定义是解题的关键.

练习册系列答案
相关题目
20. 如图,O,A,B三点在同一直线上,则下列说法中正确的是( )
如图,O,A,B三点在同一直线上,则下列说法中正确的是( )
 如图,O,A,B三点在同一直线上,则下列说法中正确的是( )
如图,O,A,B三点在同一直线上,则下列说法中正确的是( )| A. | 射线OA与射线AO表示同一条射线 | B. | 射线OA大于射线AB | ||
| C. | 射线OA与射线OB表示同一条射线 | D. | 线段OA与线段AO表示两条不同线段 |
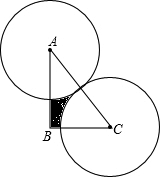 如图,在Rt△ABC中,∠ABC=90°,AB=4,BC=3,分别以A、C为圆心,以$\frac{AC}{2}$的长为半径作圆,将Rt△ABC截去两个扇形,则剩余(阴影)部分的面积为6-$\frac{25}{16}$πcm2(结果保留π)
如图,在Rt△ABC中,∠ABC=90°,AB=4,BC=3,分别以A、C为圆心,以$\frac{AC}{2}$的长为半径作圆,将Rt△ABC截去两个扇形,则剩余(阴影)部分的面积为6-$\frac{25}{16}$πcm2(结果保留π)
 甲、乙两人沿相同的路线由A地到B地匀速前进,A、B两地间的路程为20km,他们前进的路程为s(km),甲出发后的时间为t(h),甲、乙前进的路程与时间的函数图象如图所示,根据图象信息回答下列问题:
甲、乙两人沿相同的路线由A地到B地匀速前进,A、B两地间的路程为20km,他们前进的路程为s(km),甲出发后的时间为t(h),甲、乙前进的路程与时间的函数图象如图所示,根据图象信息回答下列问题: