题目内容
3.(1)如图(1),已知MA1∥NAn,探索∠A1、∠A2、…、∠An,∠B1、∠B2、…、∠Bn-1之间的关系;(2)如图(2),已知MA1∥NA4,探索∠A1、∠A2、∠A3、∠A4,∠B1、∠B2之间的关系;
(3)如图(3),已知MA1∥NAn,探索∠A1、∠A2、…、∠An之间的关系.
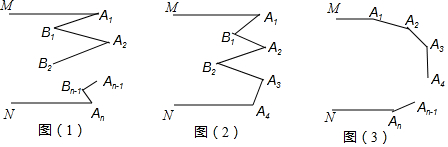
分析 (1)过点B1作B1E∥AA1,由平行线的性质证得∠A1,=∠1,∠A2=∠2,则∠A1B1A2=∠1+∠2=∠A1+∠A2,即∠A1+∠A2=∠A1B1A2.
(2)如图2,证法同上;
(3)过A2作A2B∥MA1,结合平行线的性质可得出结论,从而找到规律,利用规律解题即可.
解答  解:(1)如图1,过点B1作B1E∥AA1,则∠A1,=∠1.
解:(1)如图1,过点B1作B1E∥AA1,则∠A1,=∠1.
∵AA1∥BA2,
∴B1E∥BA2,
∴∠A2=∠2,
∴∠A1B1A2=∠1+∠2=∠A1+∠A2,即∠A1+∠A2=∠A1B1A2.
∴∠A1+∠A2+…+∠An=∠B1+∠B2+…+∠Bn-1;
(2)证法(1),∠A1+∠A2+∠A3+∠A4=∠B1+∠B2180°;
(3)过A2作A2B∥MA1,如图(3),
∵MA1∥NA3,
∴A2B∥NA3,
∴∠MA1A2+∠BA2A1=∠BA2A3+∠NA3A2=180°,
∴A1+∠A2+∠A3=360°,
同理可得∠A1+∠A2+∠A3+∠A4=540°,∠A1+∠A2+∠A3+∠A4+∠A5=720°,
∴∠A1+∠A2+∠A3++…+∠An-1=(n-2)•180°.
点评 本题主要考查平行线的性质,掌握平行线的性质和判定是解题的关键,即①两直线平行?同位角相等,②两直线平行?内错角相等,③两直线平行?同旁内角互补,④a∥b,b∥c⇒a∥c.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
13.对整式3x2-12y2因式分解正确的是( )
| A. | 3(x2-4y2) | B. | 3(x+2y)(x-2y) | C. | 3(2x+y)(2x-y) | D. | 3(x-2y)2 |
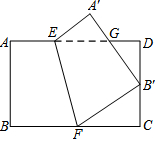 将矩形ABCD沿EF折叠,使点B与CD边中点B′重合,A′B′交AD于点G,若AE=1,AB=2,BC=3,下面有4个结论中,正确的个数是( )
将矩形ABCD沿EF折叠,使点B与CD边中点B′重合,A′B′交AD于点G,若AE=1,AB=2,BC=3,下面有4个结论中,正确的个数是( ) 如图所示,O是直线AB上的点,OD是∠AOC的平分线,OE是∠COB的平分线,∠COD=28°,求∠EOB的度数.
如图所示,O是直线AB上的点,OD是∠AOC的平分线,OE是∠COB的平分线,∠COD=28°,求∠EOB的度数.
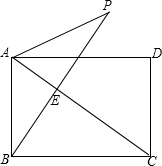 如图,矩形ABCD中,AB=6,BC=8,过点B作BE⊥AC,垂足为E,把△ABE沿AE翻折,得△APE.
如图,矩形ABCD中,AB=6,BC=8,过点B作BE⊥AC,垂足为E,把△ABE沿AE翻折,得△APE.