题目内容
8. 如图,在平面直角坐标系中,函数y=$\frac{2}{x}$(x>0)的图象经过矩形OABC的边AB、BC的中点E、F,则四边形OEBF的面积为2.
如图,在平面直角坐标系中,函数y=$\frac{2}{x}$(x>0)的图象经过矩形OABC的边AB、BC的中点E、F,则四边形OEBF的面积为2.
分析 连接OB,如图,利用反比例函数系数k的几何意义得到S△OAE=S△OCF=1,再根据三角形面积公式得到S△OAE=S△OBE=1,S△OBF=S△OCF=1,从而得到四边形OEBF的面积.
解答 解: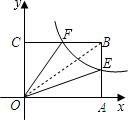 连接OB,如图,
连接OB,如图,
S△OAE=S△OCF=$\frac{1}{2}$×2=1,
∵点E、F为矩形OABC的边AB、BC的中点,
∴S△OAE=S△OBE=1,S△OBF=S△OCF=1,
∴四边形OEBF的面积=1+1=2.
故答案为2.
点评 本题考查了反比例函数比例系数k的几何意义:在反比例函数y=$\frac{k}{x}$图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.在反比例函数的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是$\frac{1}{2}$|k|,且保持不变.也考查了矩形的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.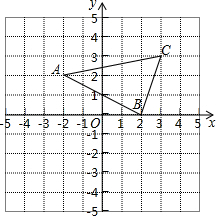 如图,已知△ABC在平面直角坐标系中的位置如图所示,将△ABC先向下平移5个单位,再向左平移2个单位,则平移后C点的坐标是( )
如图,已知△ABC在平面直角坐标系中的位置如图所示,将△ABC先向下平移5个单位,再向左平移2个单位,则平移后C点的坐标是( )
 如图,已知△ABC在平面直角坐标系中的位置如图所示,将△ABC先向下平移5个单位,再向左平移2个单位,则平移后C点的坐标是( )
如图,已知△ABC在平面直角坐标系中的位置如图所示,将△ABC先向下平移5个单位,再向左平移2个单位,则平移后C点的坐标是( )| A. | (5,-2) | B. | (1,-2) | C. | (2,-1) | D. | (2,-2) |
7.今年2月份,某市经济开发区完成出口316000000美元,将这个数据316000000用科学记数法表示应为( )
| A. | 316×106 | B. | 31.6×107 | C. | 3.16×108 | D. | 0.316×109 |
20.4的算术平方根是( )
| A. | ±2 | B. | 2 | C. | ±16 | D. | 16 |
 如图1,将边长为a的大正方形剪去一个边长为b的小正方形并沿图中的虚线剪开,拼接后得到图2,这种变化可以用含字母a,b的等式表示为a2-b2=(a+b)(a-b).
如图1,将边长为a的大正方形剪去一个边长为b的小正方形并沿图中的虚线剪开,拼接后得到图2,这种变化可以用含字母a,b的等式表示为a2-b2=(a+b)(a-b). 如图,在边长为1的小正方形构成的网格中,有一个半径为1的⊙O,且圆心在格点上,tan∠AED的值为$\frac{1}{2}$.
如图,在边长为1的小正方形构成的网格中,有一个半径为1的⊙O,且圆心在格点上,tan∠AED的值为$\frac{1}{2}$. 如图,某校有一块长为(3a+b)米,宽为(2a+b)米的长方形空地,中间是边长(a+b)米的正方形草坪,其余为活动场地,学校计划将活动场地(阴影部分)进行硬化.
如图,某校有一块长为(3a+b)米,宽为(2a+b)米的长方形空地,中间是边长(a+b)米的正方形草坪,其余为活动场地,学校计划将活动场地(阴影部分)进行硬化.