题目内容
13.有四张形状材质相同的不透明卡片,下面分别写有1、2、-1、-3四个数字.将这四张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有的数字作为一次函数y=kx+b中的k的值;第二次从余下的三张卡片中再随机抽取一张,上面标有的数字作为b的值,则使该一次函数的图象经过第一、三、四象限的概率为$\frac{1}{3}$.分析 用列表法求出所有可能,根据表格结合概率公式求出概率.
解答 解:列表如下:
| -3 | -1 | 1 | 2 | |
| -3 | (-1,-3) | (1,-3) | (2,-3) | |
| -1 | (-3,-1) | (1,-1) | (2,-1) | |
| 1 | (-3,1) | (-1,1) | (2,1) | |
| 2 | (-3,2) | (-1,2) | (1,2) |
∴符合条件的k、b的值有:(1,-3)、(1,-1)、(2,-3)、(2,-1)四种情况,
则使该一次函数的图象经过第一、三、四象限的概率为$\frac{4}{12}$=$\frac{1}{3}$,
故答案为:$\frac{1}{3}$.
点评 本题考查了列表法与树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.也考查了一次函数函数图象上点的坐标特征.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.科学家在实验中检测出某微生物细胞直径约为0.0000035米,将0.0000035用科学记数法表示为( )
| A. | 3.5×1 0-6 | B. | 3.5×1 06 | C. | 3.5×1 0-5 | D. | 35×1 0-5 |
15.与$\sqrt{17}$最接近的整数为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
18.下列四边形中不一定为菱形的是( )
| A. | 对角线相等的平行四边形 | |
| B. | 每条对角线平分一组对角的四边形 | |
| C. | 对角线互相垂直的平行四边形 | |
| D. | 用两个全等的等边三角形拼成的四边形 |
3.已知(x1,y1)和(x2,y2)是直线y=-3x上的两点,且x1<x2,则y1与y2的大小关系是( )
| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 以上都有可能 |
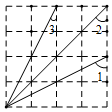 在如图所示的4×4正方形网格中,∠1+∠2+∠3=135°.
在如图所示的4×4正方形网格中,∠1+∠2+∠3=135°. 如图,在平面直角坐标系中,函数y=$\frac{2}{x}$(x>0)的图象经过矩形OABC的边AB、BC的中点E、F,则四边形OEBF的面积为2.
如图,在平面直角坐标系中,函数y=$\frac{2}{x}$(x>0)的图象经过矩形OABC的边AB、BC的中点E、F,则四边形OEBF的面积为2. 如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE,已知菱形ABCD的周长为20cm,则 OE长为5cm.
如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE,已知菱形ABCD的周长为20cm,则 OE长为5cm. 如图,宽为50的大长方形是由10个形状相同、大小相等的小长方形拼成,其中一个小长方形的面积为400.
如图,宽为50的大长方形是由10个形状相同、大小相等的小长方形拼成,其中一个小长方形的面积为400.